Доказательная история, 6-я серия - Реальные размеры Земли

У историков всё просто: плавать без компаса - просто, соорудить гигантские пирамиды - просто, делать бронзу без олова - просто. Причём, чем древнее эпоха, тем больше допущений позволяют себе историки, удивляет только, как они ещё не додумались до инопланетян, ведь это сразу бы многое объяснило. Впрочем, вернёмся к сути. Одной из наилегчайших задач в истории человечества, по мнению историков, была задача определения реальных размеров Земли. Для этого надо было всего лишь измерить высоту тени в двух городах и по разнице вычислить радиус. 

Читаем википедию:

В тесной связи с астрономией находится работа Эратосфена, состоящая в измерении длины земного меридиана. Краткое изложение этой работы известно нам по трактату Клеомеда «О круговращении небесного свода»:

Ого на что замахнулся! Длину земного меридиана измерить!!! Вся элита европейской науки билась над этой загадкой с 15 по 17 века, а Эратосфен её решил одним мизинцем. Даже Колумб, отправляясь в плавание, не знал реальных размеров Земли.

Полагают, что ещё в 1474 году астроном и географ Паоло Тосканелли сообщил Колумбу в письме, что до Индии можно добраться гораздо более коротким морским путём, если плыть на запад. По-видимому, уже тогда Колумб задумался о своём проекте морского путешествия в Индию. Возможно, на заниженную оценку Колумбом размеров Земли повлиял труд Imago Mundi (лат. Картина Мира, 1410) епископа Петра де-Аллиако[4][5]. Произведя собственные расчёты на основании карты Тосканелли, он решил, что удобнее всего плыть через Канарские острова, от которых до Японии, по его мнению, оставалось около пяти тысяч километров.

...

Христофор Колумб заблуждался, не зная реальных размеров Земли и считая, что она гораздо меньше. К тому же в то время считалось, что в основном нашу планету покрывает суша. Поэтому Колумб решил, что сможет найти более короткий путь в Азию, проплыв на запад. И даже высадившись на американский берег, он еще долго считал, что достиг берегов Восточной Азии.

...

В последующие за тем Средние века не только не производилось других градусных измерений, но забыта была сама мысль о шарообразности Земли, и следующая попытка сделана была уже в 1525 г. французским врачом Фернелем. Он измерил дугу меридиана между Парижем и Амьеном по счету оборотов колеса своего экипажа, а высоты солнца на конечных точках деревянным треугольником с диоптрами. Главные ошибки всех этих градусных измерений проистекали от неверного измерения линейной длины выбранных дуг; непосредственным измерением нельзя точно получить большое расстояние, особенно на неровной местности.

Эпоху в развитии градусных измерений составляет работа голландского математика Снеллиусав 1616—17 гг. Он заменил непосредственное измерение длинной дуги на земной поверхности триангуляцией, состоящей в проложении ряда смежных треугольников, в которых измеряют только все углы и длину какой-нибудь одной стороны. Такую сторону, называемую базисом, сравнительно небольшой длины, всегда можно выбрать на ровной, удобной для измерения местности. Измерение же углов — работа несравненно более простая. Зная одну сторону и все углы, нетрудно по правилам тригонометрии вычислить все прочие стороны, а затем и расстояния между конечными пунктами триангуляции. Снеллиус проложил 32 треугольника между Алкмаром и Бергеном в окрестностях Лейдена и получил для длины одного градуса величину 28500 голландских рут, или 55100 туазов, что, как впоследствии оказалось, было слишком мало. Ошибочность вывода произошла главным образом от несовершенства измерительных снарядов: длину базиса он измерил простою железною линейкою, а углы — медным квадрантом с диоптрами, позволявшими отсчитывать только минуты дуги. Однако основания нового способа были совершенно верны, и с тех пор все последующие градусные измерения состояли именно в проложении системы треугольников, в которых измерялась одна или две (для поверки) небольшие стороны.

Первым подражателем Снеллиуса был французский математик и астроном Пикар. Он проложил в 1669—70 годах триангуляцию между Амьеном и Мальвуазеном и получил для длины одного градуса меридиана величину 57060 туазов, что весьма близко к истине. На этой триангуляции впервые были применены усовершенствованные угломерные снаряды со зрительными трубами, снабженными сетками нитей в окулярах. Градусное измерение Пикара в историческом отношении замечательно тем, что оно послужило И.Ньютону основанием в его работах, приведших к открытию законов всемирного тяготения.

Триангуляция, угломерные снаряды со зрительными трубами... ничего этого Эратосфену не требовалось, он как-то без всего этого справился. Но, вернёмся к гревним дрекам, о том, что они там вытворяли можно читать только с открытым ртом:

Эратосфен говорит, что Сиена и Александрия лежат на одном меридиане. И поскольку меридианы в космосе являются большими кругами, такими же большими кругами обязательно будут и меридианы на Земле. И поскольку таков солнечный круг между Сиеной и Александрией, то и путь между ними на Земле с необходимостью идёт по большому кругу.

Я теперь понимаю, почему именно математики восстали против историков и создали "Новую хронологию". Представляю как у них полыхали пятые точки, когда они читали такие явные исторические подлоги.

Во-первых, - с чего Эратосфен вообще взял, что Александрия и Сиена находятся на одном меридиане???

Во-вторых, какими такими способами он вообще мог в то время вычислять меридианы?

Одним из первых способ определения долготы предложил известный путешественник Америго Веспуччи, посвятивший много времени и сил изучению проблемы во время своего пребывания в Новом Свете:

Что касается долготы, я заявляю, что обнаружил, что при её определении я столкнулся с большими трудностями, и мне пришлось очень сильно постараться выяснить расстояние между востоком и западом, которое я преодолел. Конечным результатом моих трудов было то, что я не нашёл ничего лучше, чем наблюдать в ночное время за соединением одной планеты с другой, и особенно за соединением Луны с другими планетами, потому что Луна быстрее в её ходе, чем любая другая планета. Я сравнил свои наблюдения с альманахом. После того, как я провёл эксперименты много ночей, однажды ночью, двадцать третьего августа 1499 года, произошло соединение Луны с Марсом, которое, согласно альманаху, должно было произойти в полночь или полчаса назад. Я обнаружил, что … в полночь положение Марса было три с половиной градуса к востоку

Наряду с методом Веспуччи, было предложено ещё несколько астрономических методов измерения долготы — Иоганна Вернера (метод лунных расстояний[en], с XVI по начало XX века[2]), Галилео Галилея (по положению спутников Юпитера, 1612 год), — но для их реализации требовались сложные астрономические инструменты и вычисления. Более простой способ, изобретение которого приписывают Фризиусу Гемме — сравнение местного солнечного времени с точным в референсной точке (порту) — требовал очень точных часов.

В 1714 году британский парламент предложил огромную премию за разработку метода определения долготы — 10 000 фунтов за метод определения долготы с погрешностью в пределах одного градуса большого круга Земли, то есть в пределах 60 морских миль, 15 000 фунтов, если погрешность будет менее двух третей этого расстояния, 20 000 фунтов, если она будет менее половины этого расстояния[3]. Для определения долготы с такой погрешностью во время плавания в Вест-Индию требовались часы со среднесуточным уходом не более 3 секунд (при том, что часы в то время считались очень точными, если вообще имели минутную стрелку)[4].

Как мы видим, для определения долгот, Америго Веспуччи использовал альманах, иными словами - астрономические таблицы, которые составляли видные астрономы Европы. А чем пользовался Эратосфен? Каким макаром он вообще мог вычислять долготы и знать на каком меридиане какой город находится?

К слову, Александрия и Сиена, то бишь - Асуан, не лежат на одном меридиане:

Александрия находится на 30 градусах восточной долготы, а Асуан почти на 33. Разница почти в три градуса.

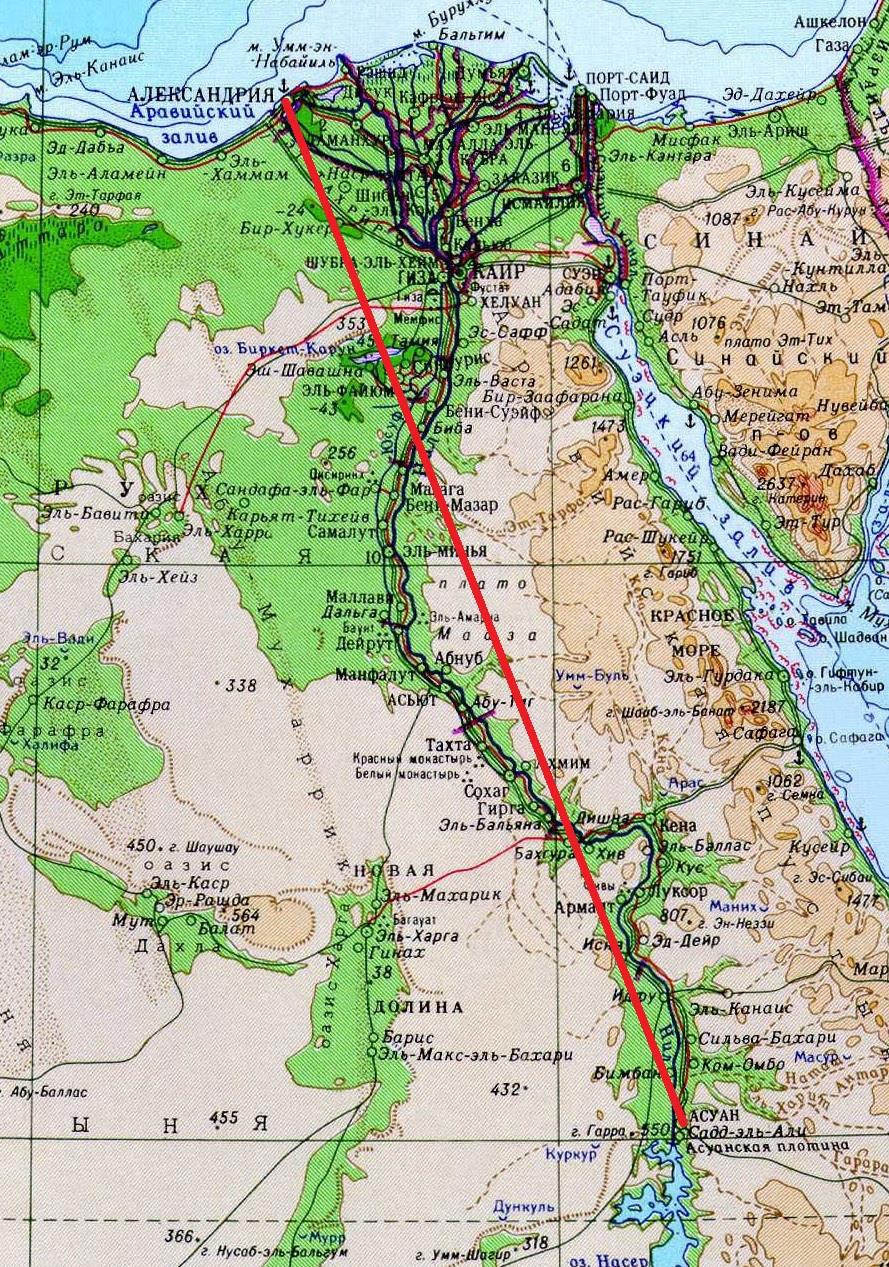
Далее следует стандартная школьная история, про то, что в полдень, в день летнего солнцестояния на широте северного тропика исчезает тень, тогда как на широте Александрии, в тот же день, тень не исчезает. В интере гуляет много однообразных картинок на эту тему:

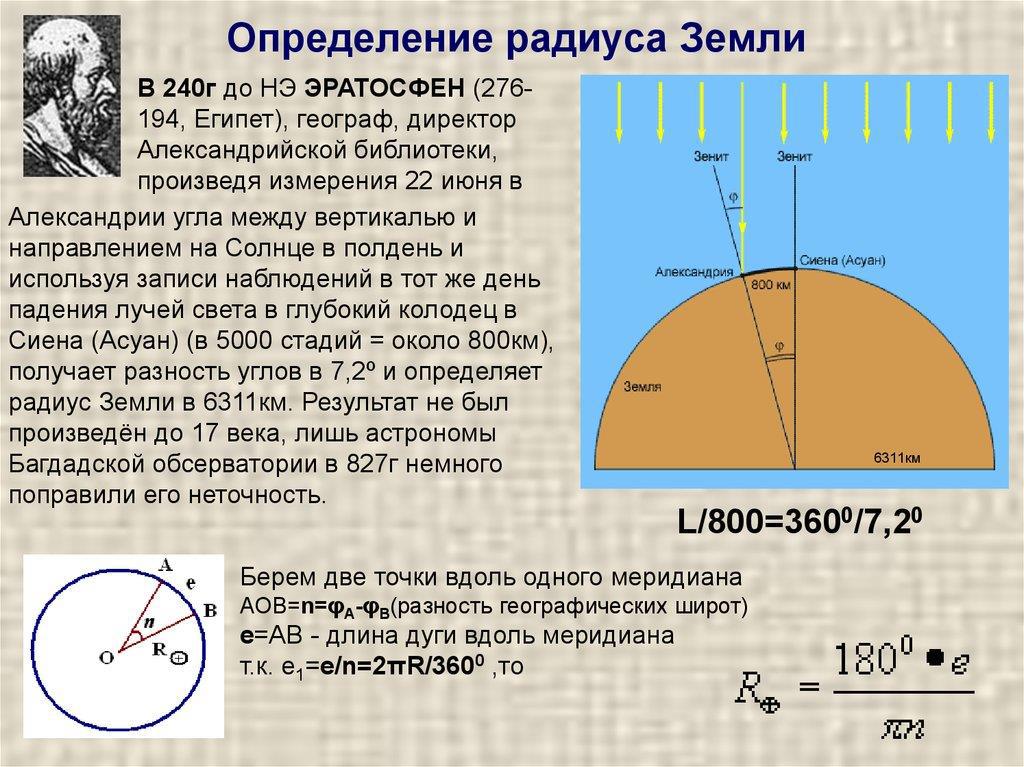
И всё вроде бы выглядит гладко, вот только, откуда Эратосфен взял, что от Александрии до Сиены 5000 стадий? Как он мог измерить это расстояние? И с чего он взял, что такую кривую загагулину, которой являлся путь из Александрии в Сиену, можно использовать в геометрических вычислениях???

Мало того, что, как мы выяснили, эти два города не лежат на одном меридиане, так вы ещё и взгляните, что из себя представляет путь из Александрии в Сиену:

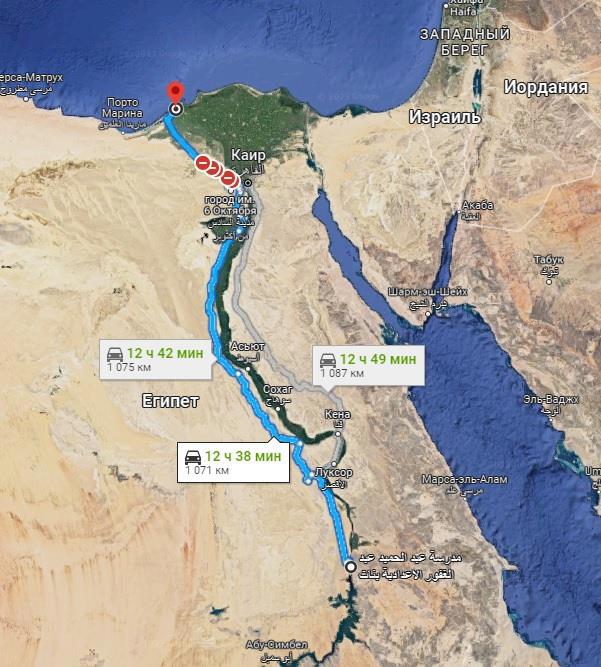
Это очень далеко от прямой линии, которую можно было бы использовать в геометрии. И о каких 800 километрах идёт речь? По современным дорогам под 1100 км выходит, а по Нилу, так ещё больше. Да, даже если провести прямую линию между двумя этими городами (а фабриканты этого подлога, скорее всего так и делали), то получается расстояние свыше 800 км, в частности - 844 км.

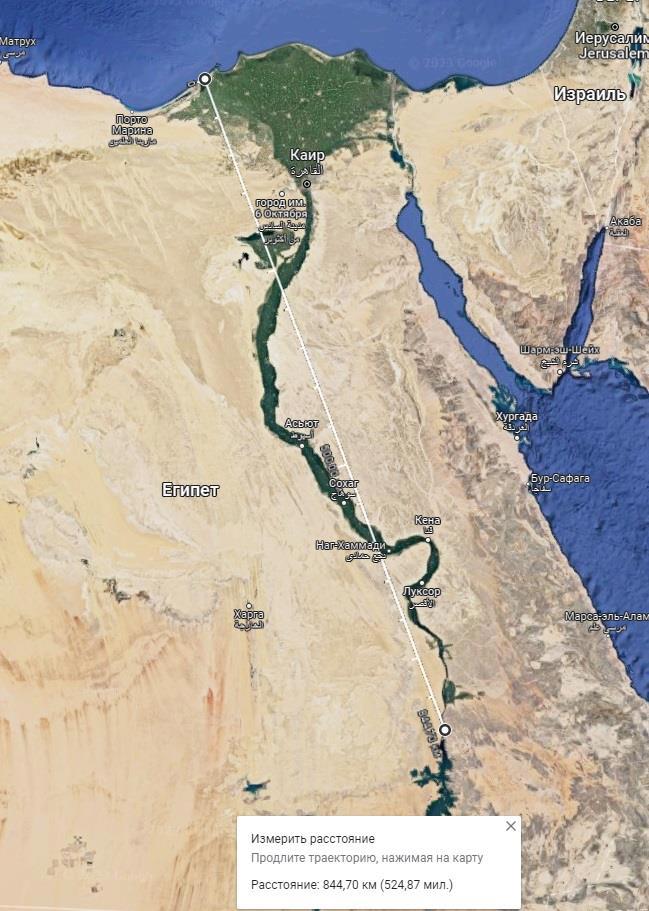
И как только при таких погрешностях Эратосфену удалось так точно вычислить радиус Земли?

Позднее полученное Эратосфеном число было увеличено до 252 000 стадиев. Определить, насколько эти оценки близки к реальности, трудно, поскольку неизвестно, каким именно стадием пользовался Эратосфен. При значении стадия от 209,4 метров (стадий системы фараонов) до 178 (греческого) и 172,5 (египетский) значения радиуса могли колебаться от 8 397 км до 6 916 км. Также упоминают использования стадия в размере 157,2 метра, при котором радиус Земли равнялся бы 6 302 км[7]. Современные измерения дают для усреднённого радиуса Земли величину 6 371 км, что в любом случае делает вышеописанный расчёт выдающимся достижением и первым достаточно точным расчётом размеров нашей планеты.

Более того, Эратосфену ещё и приписывают изобретение картографии, да не просто картографии, а создание карты мира!

Считается, что именно Эратосфен создал первую карту мира, которая давала примерное представление о взаимной удаленности городов и стран. Он утверждал, что точное отображение мира, даже в двух измерениях, зависит только от установления точных линейных размеров. Его великие достижения в области картографии сразу стали использоваться в качестве новой методики для построения карт с меридианами, и параллелями.

Кем считается, не понятно. И как он собрался точно отобразить земной шарик в двух измерениях, остаётся загадкой. Но создание карт, в эпоху, когда ещё никто не умел вычислять долготы, когда не было даже элементарного компаса, выглядит уже откровенным бредом. Естественно, что никакого оригинала данной карты не сохранилось и нам придётся в очередной раз поверить на слово историкам. 

Но какой итог мы могли бы подвести под вышесказанным?

Для создания грамотных исторических подлогов надо хорошо знать много других наук, главным образом, астрономию и математику. Личности, которые лепили данные фальсификации, особым умом не отличались, поэтому допускали такие ляпы и косяки. Но меня поражает упорство, с которым историки пытаются насытить древний мир технологиями, ему не свойственными, очевидно, рассчитывая на то, что никто не полезет копать и проверять их бредни.

Был ли Эратосфен на самом деле, значения не имеет, имеет значение лишь последовательность, с которой возникают и применяются технологии. Нельзя сначала изобрести джойстик, затем, через 300 лет - дисковод, после чего через 500 лет процессор и ещё через 800 лет собрать первую игровую приставку. А у историков всё выглядит именно так. 

Спасибо за внимание