Интересные детали в дополнение египетско-географической версии

Данный блог является продолжением серии блогов, посвящённых расследованию тайн великих пирамид и зарождению древней географии. Если вы их не читали то, скорее всего, вы здесь нихрена не поймёте

Итак, первое, на что хотелось бы обратить внимание, это на большое количество арабских учёных, которые в средние века свалились на человечество словно снег на голову, а потом так же внезапно исчезли. Что это было? Зачем вообще арабам заниматься математикой и астрономией? Дело в том, что их просто не к чему прилепить. Ну нет никаких оснований у арабов заниматься математикой, у них от неё что, пшеница лучше расти будет? Астрономия им вообще была до лампочки, потому как астрономический год не синхронизируется с климатическими временами года. Нельзя при помощи астрономии вычислить ни засуху, ни ливень, ни начало весны, ни окончание лета, все эти явления плавают в определённом промежутке времени и их закономерности до сих пор не могут разгадать метеорологи, а чего уж говорить про те времена, когда и науки то такой как метеорология не было?

Но учёные арабские есть и это факт, с которым нельзя спорить. Более того, большое количество научных терминов происходят из арабского языка, да даже цифры у нас, вроде как, арабские. Как так получается? У них что, было какое-то временное помутнение рассудка из-за которого они тут же кинулись заниматься науками?

Если же мы будем исходить из версии, что во временном промежутке позднего средневековья - эпохи возрождения шли глобальные исследования по созданию карты мира, то логично предположить, что учёных брали там же, где и проводились исследования. Мы же не верим в расовую теорию, что одни расы умственно превосходят другие? Поэтому, если математические исследования мог проводить голландец, то почему их не мог проводить араб? Кому заплатили, тот и занимался наукой. Причём, арабские учёные могли обходиться дешевле. Сейчас такое явление называют - "аутсорсинг". И если сейчас программы для гугла пишут индусы, то почему в средние века математическими исследованиями для мировых шишек не могли заниматься арабы?

Ну а кто, собственно, финансировал эту лавочку? Я уже писал об этом в одном из прошлых блогов. Изначально карта мира нужна была купцам, точнее, не карта мира, а карта торговых путей. Создание карты мира и возникновение государств благодаря географии это побочные явления от изначальной затеи купцов создать себе карты маршрутов.

Соответственно, когда доступ к картам получили местные вожди, они начали организовывать свои первые государства и заниматься "собиранием земель". Причём, некоторые государства возникали непосредственно на основе купеческих компаний - Голландская Ост-Индская компания, Британская Ост-Индская компания и т. д. То есть, купцы в древнем мире имели колоссальный политический вес и фактически были высшим сословием.

Ну и, раз пирамиды строили в арабском Египте, то и людей для произведения расчётов брали там же. 

Следующий момент, на который я бы хотел обратить внимание это то, что на первых картах отсутствует один очень важный элемент, который есть на всех современных картах. Этот элемент - масштаб, точнее, - масштабная линейка. 

Никакого масштаба нет на этой карте, которую можно назвать первой картой мира. 

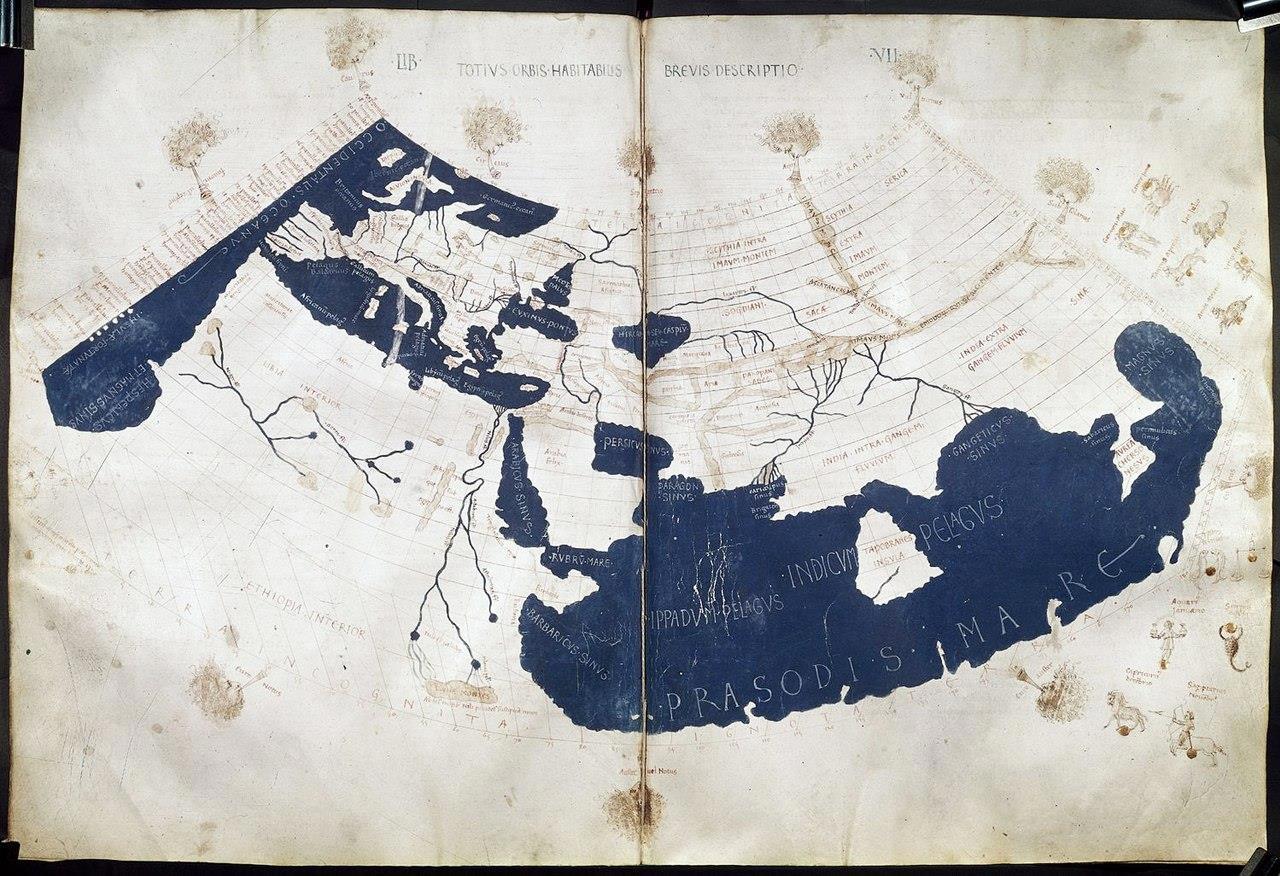
На одной из её последующих копий есть достаточно точная разбивка по широтам и долготам, но масштабной линейки так же нет. 

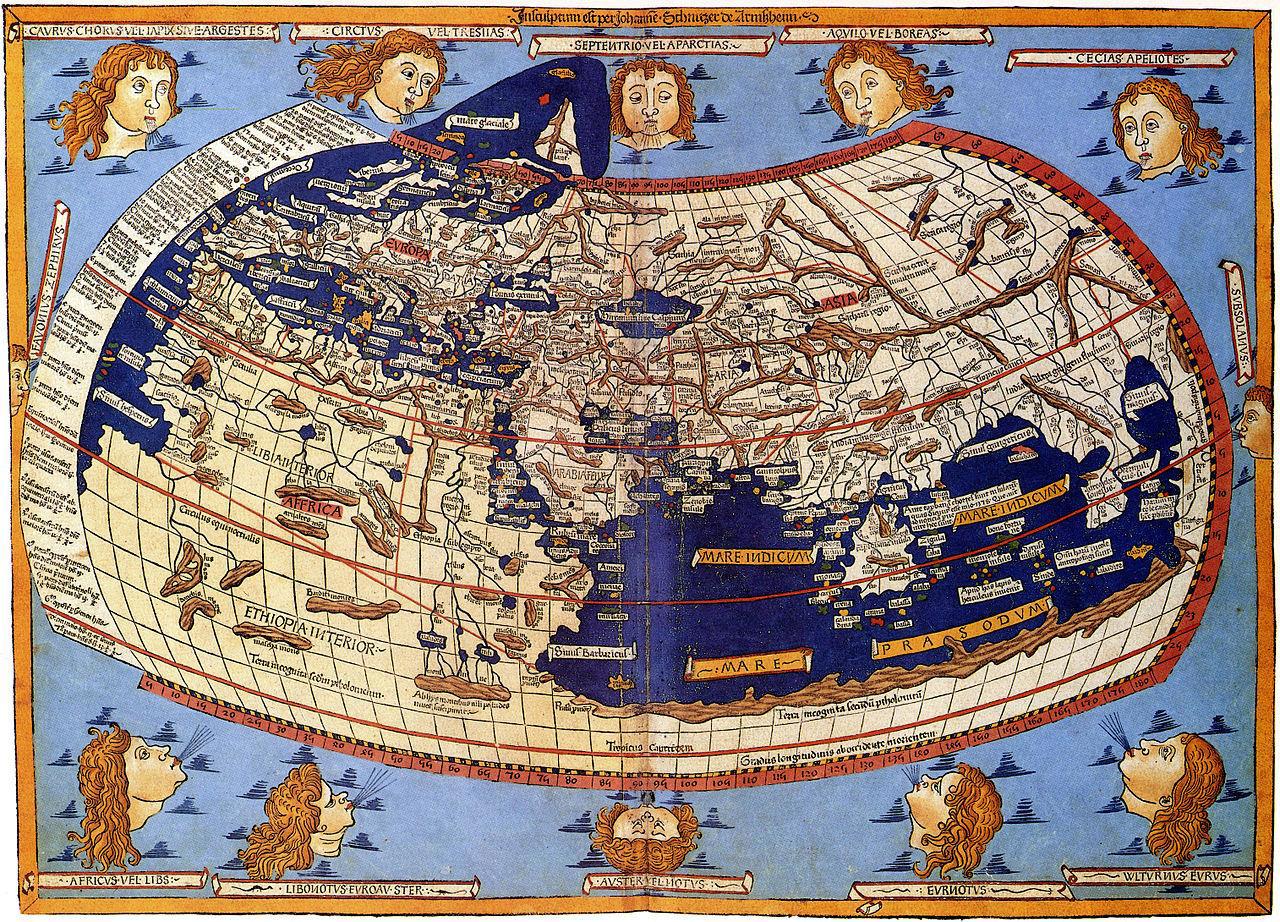
Нет масштабной линейки и на этой карте Абрахама Ортелиуса, созданной в 1570 году. 

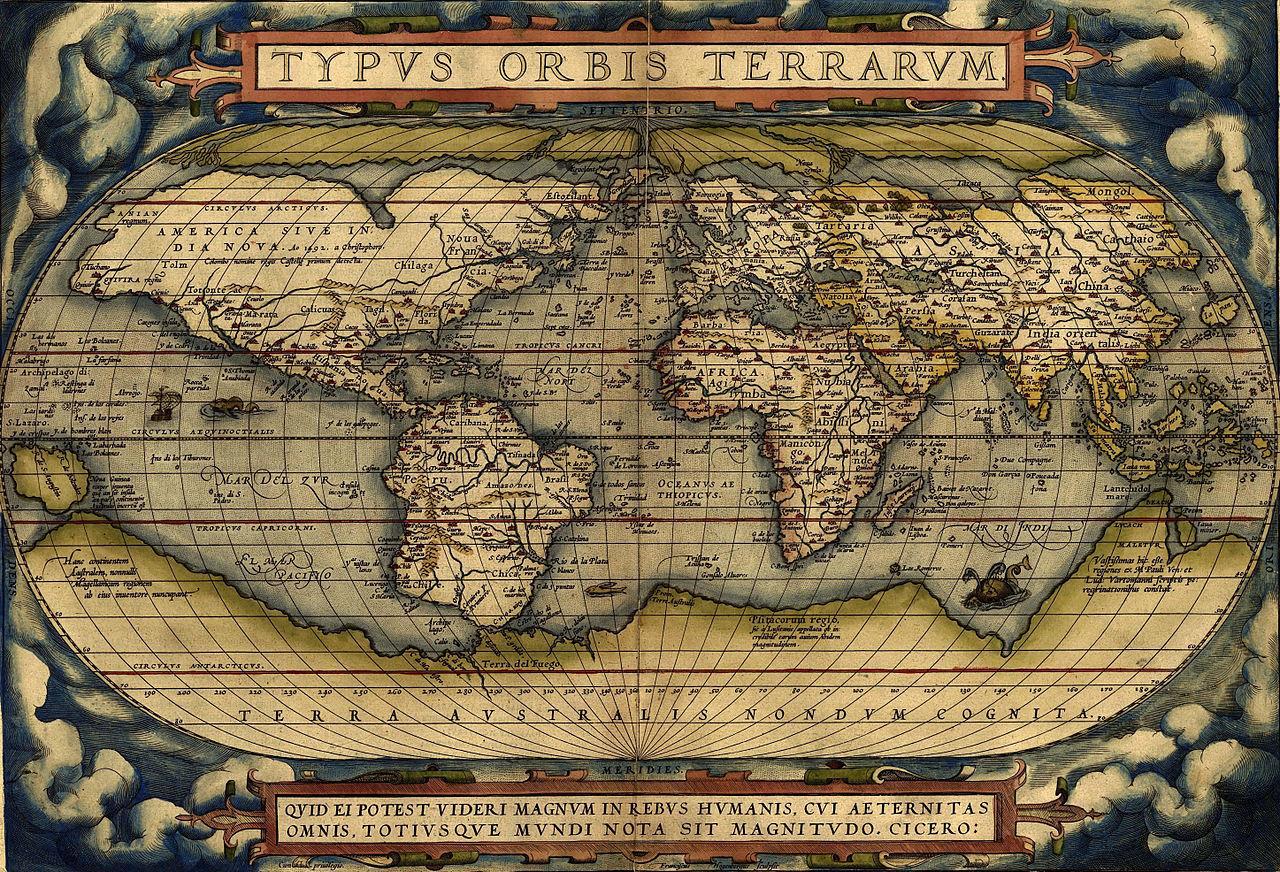
Но почему так получается? Почему на первых картах нет масштабных линеек? А всё очень просто, - люди не знали реальных размеров Земли, поэтому и масштабировать было нечего. Широту и долготу определять научились, но не более того. Поэтому, чему равен один градус широты, оставалось только догадываться. 

Впервые, масштабная линейка появляется на картах Меркатора. 

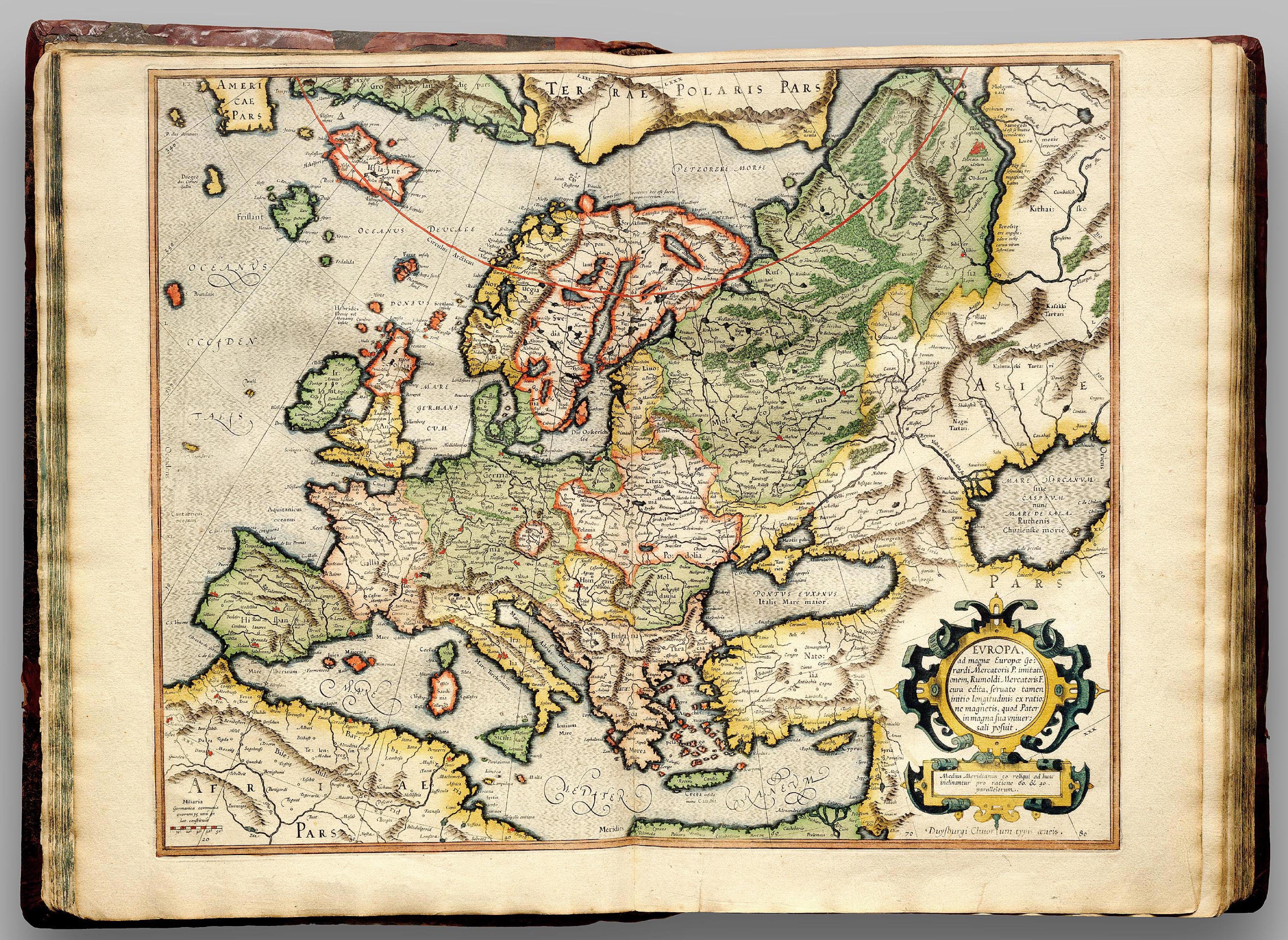
Здесь мы можем видеть, как она подписана:

Если кому плохо видно, то фраза выглядит так: Miliaria germanica communia quorum 15 gradum unum latitudinis constituunt

гугл перевод с латыни: "обычные германские мили, из которых 15 составляют один градус широты"

Правда, вот незадача. Атлас свой Меркатор издал в 1595 году, а размеры Земли удалось вычислить только в 1617. Как так получается? Откуда он знал сколько германских милей в одном градусе, если он никак не мог знать, чему равняется длина меридиана? 

Тут следует отметить, что длину меридиана вычислил человек с именем, которое невозможно выговорить:

Виллеброрд Снеллиус 

Причём, он не просто вычислил длину меридиана, а создал метод которым пользуются по сей день - триангуляция. Без триангуляции и угломерных приборов ничего вычислить в принципе было нельзя. Вот что пишет о расчётах Снеллиуса википедия:

В результате своих расчётов Снелл получил хорошую оценку окружности Земли — в переводе на метрическую систему: 38653 км (ошибка 3,5 %).

То есть, он получил очень точное значение для той эпохи. Но о каких милях тогда ведёт речь Меркатор? Тут я позволю себе предположить, что Меркатор и не должен был знать, чему равняется германская миля. И в данном случае, он использовал мили лишь как относительную меру, чтобы понимать разницу расстояний. 

Более того, Меркатор мог не знать, чему равняется длина меридиана, но он мог знать, что ведётся подготовка к точному измерению длины меридиана и для этого специально строится комплекс пирамид в Гизе. Таким образом, Меркатор знал, что уже буквально через несколько десятилетий учёным удастся вычислить этот параметр. И, в какой-то мере, он указывал свои германские мили на картах авансом, понимая, что картами его будут пользоваться ещё долгое время. 

В прошлом блоге я предположил, что для измерения длины меридиана при помощи пирамид нужен очень большой квадрант и такой квадрант нашёлся, собственно, это и есть квадрант Снеллиуса:

Высота 210 см, разметка шкалы до 1/10 градуса. При помощи такого квадранта, проведя замеры в районе великих пирамид можно вычислить длину меридиана. Но я сказал бы, что это минимальный размер такого квадранта. Вообще, я надеялся, что квадрант будет немного побольше. К тому же, у Меркатора миля это 1/15 градуса, следовательно квадрант должен быть размечен как-минимум до 1/30, а лучше до 1/60. Но такой квадрант будет уже как минимум раза в три больше и при транспортировке с места на место его придётся разбирать и собирать каждый раз заново, а потом ещё и калибровать. 

Хотя, учитывая какую погрешность дали расчёты Снеллиуса, можно предположить что перед нами тот самый квадрант, которым и проводились измерения в Гизе. 

Ну и в заключение хочу добавить, что в прошлых блогах я предполагал, что пирамиды были построены в 18-м веке, а тут, получается, 17-й, - ошибка в сто лет? На это у меня есть версия, что пирамиды были построены в 17-м, а пользовались ими для измерений вплоть до конца 18-го, до тех пор, пока не была принята метрическая система. Помимо длины меридиана ещё нужно было решить вопрос о форме Земли. Поэтому, строительство пирамид было продолжено и на них продолжали делать измерения, хотя, это уже был и не основной метод. 

Спасибо за внимание