Про людей не знающих, но с очень большим ЧСВ!

я по образованию - инженер. не могу сказать что "тервер" был всегда моей самой сильной стороной, но взять школьную задачку, приложить к ней школьные же формулы и методы решения я всё же способна. (да, я так же полагаю что школьная задачка должна решаться школьными методами, а не институтскими!) но тут возник ньюанс...

есть человек, который выложил задачку (а я такое очень люблю!):

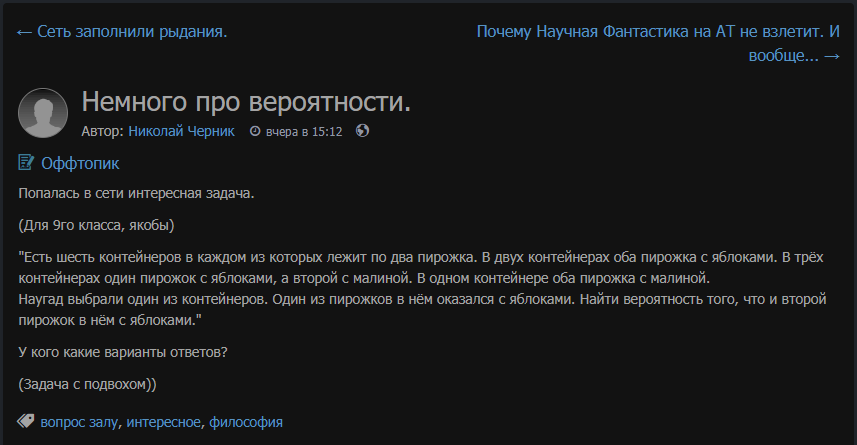
и под этим постом один человек выложил свое "решение":

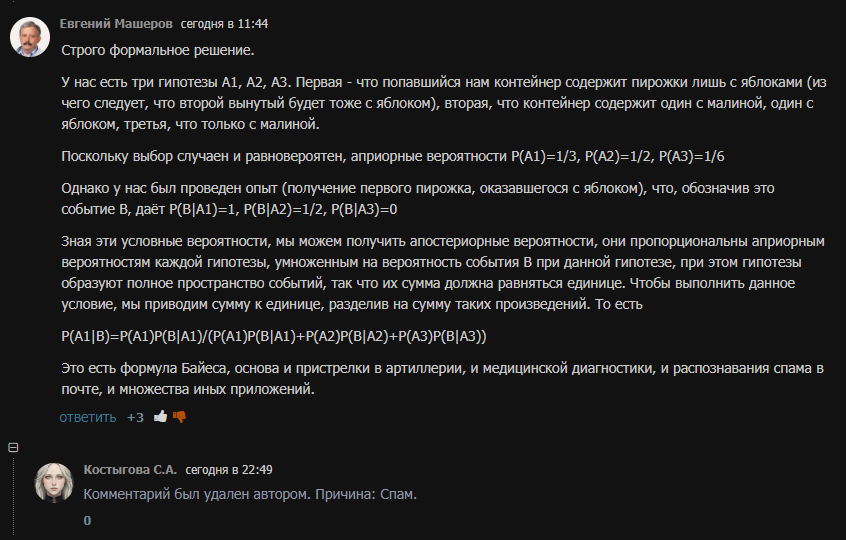
проблема приведенного решения в том, что он (всего на всего) НЕ РЕШАЕТ ПОСТАВЛЕННУЮ ЗАДАЧУ!

его решение отвечает на вопрос: какова вероятность того что взятый пирожок из контейнеров где есть яблоки будет с яблоком? просто взятый, а не второй по очереди. то есть человек решил (хоть и правильно), но совершенно принципиально ДРУГУЮ задачу. 

Да, на скрине видно что мой комментарий, где было это указанно удалили как "спам". То есть человек настолько не понимает сути простой школьной задачи, что когда ему указывают на то что он решает совсем другое, он, ради своего ЧСВ просто трет чужие комментарии! 

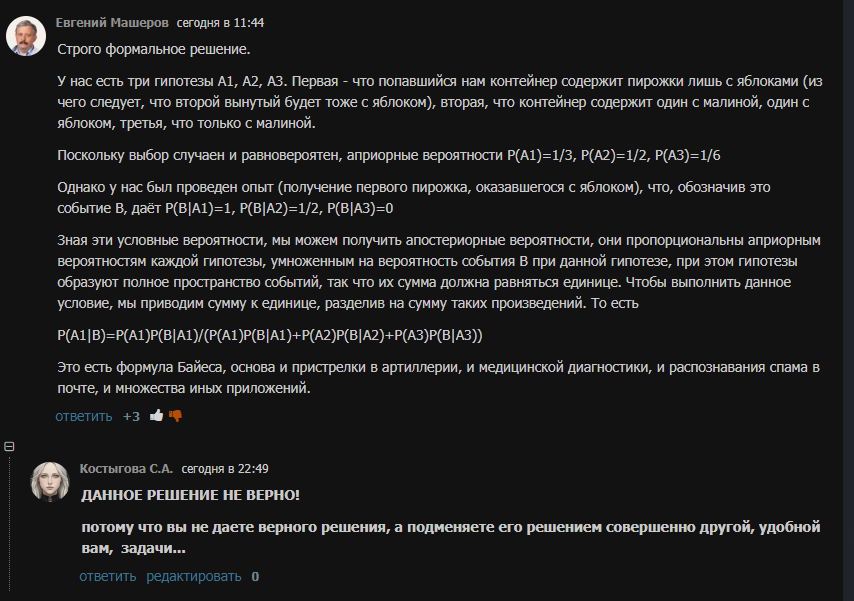
вот этот же скрин, сделанный несколькими минутами ранее...

А теперь давайте разбираться с самой задачей:

Дано:

6 контейнеров по 2 пирожка каждый. 

в 2х контейнерах по 2 пирожка с яблоком: "яя"

в 3х контейнерах 1 яблоко и 1 малина: ям

в 1м контейнере 2 с малиной: мм

после того как мы в случайно выбранном контейнере взяли в руки один из пирожков, выяснилось что он с яблоком.

Вопрос:

какова вероятность того, что второй пирожок в этом контейнере тоже с яблоком?

Решение:

Изначальный массив выглядит как:

яя, яя, ям, ям, ям, мм

после того как мы в случайно выбранном контейнере взяли в руки один из пирожков и выяснилось что он с яблоком, контейнер с 2мя пирожками с малиной покидает выборку! - тк это точно не он! в итоге у нас один пирожок заявлен как 100% с яблоком и массив выборки теперь выглядит так:

яя, яя, ям, ям, ям

тк нас, по вопросу в задании, интересует ВТОРОЙ пирожок (про первый мы и так знаем что он 100% яблоко), то по 1 яблоку из каждой клетки массива мы можем убрать. тем самым мы получаем массив:

я, я, м, м, м

это обычный простейший линейный массив, в котором мы должны посчитать вероятность (читай процент от общего числа), одного из вариантов. сумма всех вариантов = 5. сумма требуемых вариантов =2. 

соответственно количество нужных вариантов делим на общее количество: 2/5.

Ответ: 2/5

Внимание встречный вопрос:
Чего не хватает Николаю и Евгению для признания своей ошибки, если они трут посты тех, кто просто на нее указали?

Ладно я со своим МПГУ (и пофиг что ведущий педвуз страны), но человеку не смог доказать что он ошибается даже Физмат МГУ! Это какой величины должен быть ЧСВ? с таким вообще ходить можно?