Правильные многогранники

Автор: Xpath

***

Статья

***

Правильные многогранники

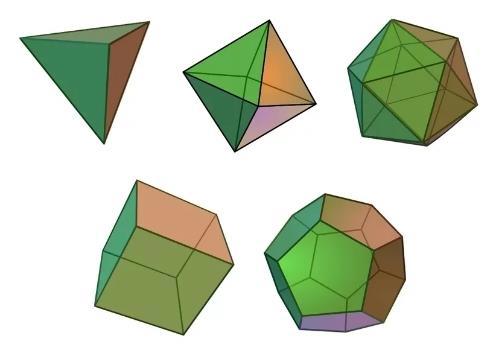
Правильный многогранник или плато́ново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.

В трёхмерном евклидовом пространстве существует всего пять правильных многогранников (упорядочены по числу граней):

упорядочены по числу граней):

Правильный многогранник	Число вершин	Число рёбер	Число граней	Число сторон у грани	Число рёбер, примыкающих к вершине	Тип пространственной симметрии
тетраэдр	4	6	4	3	3	Td
гексаэдр	8	12	6	4	3	Oh
октаэдр	6	12	8	3	4	Oh
додэкаэдр	20	30	12	5	3	Ih
икосаэдр	12	30	20	3	5	Ih

Правильный многогранник может быть комбинаторно описан символом Шлефли {p, q}, где:
p — число рёбер в каждой грани; q — число рёбер, сходящихся в каждой вершине.

Символы Шлефли для правильных многогранников приведены в следующей таблице:

Много-гранник	Вер- шины	Рёб-ра	Гра-ни	символ Шлефли
тетраэдр	4	6	4	{3, 3}
гексаэдр (куб)	8	12	6	{4, 3}
октаэдр	6	12	8	{3, 4}
додэкаэдр	20	30	12	{5, 3}
икосаэдр	12	30	20	{3, 5}

Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.

В значительной мере правильные многогранники были изучены древними греками. Некоторые источники (такие как Прокл Диадох) приписывают честь их открытия Пифагору. Другие утверждают, что ему были знакомы только тетраэдр, куб и додекаэдр, а честь открытия октаэдра и икосаэдра принадлежит Теэтету Афинскому, современнику Платона. В любом случае, Теэтет дал математическое описание всем пяти правильным многогранникам и первое известное доказательство того, что их ровно пять.

Правильные многогранники характерны для философии Платона, в честь которого и получили название «платоновы тела». Платон писал о них в своём трактате Тимей (360г до н. э.), где сопоставил каждую из четырёх стихий (землю, воздух, воду и огонь) определённому правильному многограннику.

Огню соответствовал тетраэдр,

земле — гексаэдр,

воздуху — октаэдр,

воде — икосаэдр.

Данные сопоставления пояснялись следующими ассоциациями: жар огня ощущается чётко и остро, как пирамидки-тетраэдры; мельчайшие компоненты воздуха октаэдры настолько гладкие, что их с трудом можно почувствовать; вода выливается, если её взять в руку, как будто она сделана из множества маленьких шариков, к которым ближе всего икосаэдры; в противоположность воде, совершенно непохожие на шар кубики-гексаэдры составляют землю, которые являются причиной того, что земля рассыпается в руках, в противоположность плавному току воды. По поводу пятого элемента, додекаэдра, Платон сделал смутное замечание: «…его бог определил для Вселенной и прибегнул к нему в качестве образца».

Аристотель добавил пятый элемент — эфир — и постулировал, что небеса сделаны из этого элемента, но он не сопоставлял его платоновскому пятому элементу.

Евклид дал полное математическое описание правильных многогранников в последней, XIII книге Начал. Предложения 13—17 этой книги описывают структуру тетраэдра, октаэдра, куба, икосаэдра и додекаэдра в данном порядке. Для каждого многогранника Евклид нашёл отношение диаметра описанной сферы к длине ребра. В 18-м предложении утверждается, что не существует других правильных многогранников. Математик из Базельского университета Андреас Шпейзер отстаивал точку зрения, что построение пяти правильных многогранников является главной целью дедуктивной системы геометрии в том виде, как та была создана греками и канонизирована в «Началах» Евклида[2]. Большое количество информации XIII книги «Начал», возможно, взято из трудов Теэтета.

В XVI веке немецкий астроном Иоганн Кеплер пытался найти связь между пятью известными на тот момент планетами Солнечной системы (исключая Землю) и правильными многогранниками. В книге «Тайна мира», опубликованной в 1596 году, Кеплер изложил свою модель Солнечной системы. В ней пять правильных многогранников помещались один в другой и разделялись серией вписанных и описанных сфер.

Каждая из шести сфер соответствовала одной из планет (Меркурию, Венере, Земле, Марсу, Юпитеру и Сатурну). Многогранники были расположены в следующем порядке (от внутреннего к внешнему): октаэдр, за ним икосаэдр, додекаэдр, тетраэдр и, наконец, куб. Таким образом, структура Солнечной системы и отношения расстояний между планетами определялись правильными многогранниками. Позже от оригинальной идеи Кеплера пришлось отказаться, но результатом его поисков стало открытие двух законов орбитальной динамики — законов Кеплера, — изменивших курс физики и астрономии, а также правильных звёздчатых многогранников (тел Кеплера — Пуансо).

***

Звездчатые формы и соединения тел Платона. Кроме правильных выпуклых многогранников существуют и правильные выпукло-вогнутые многогранники. Их называют звездчатыми (самопересекающимися). Рассматривая пересечения продолжения граней Платоновых тел, мы будем получать звездчатые многогранники.