Высказывания Великих людей. Рамануджан (Сринива́са Рамануджан Айенго́р)

***

Статья

***

N.B.  На днях вышел мой пост о Индии. Это пост нес некоторый оттенок негатива. Нищета, грязь, жутчайшая перенаселенность в масштабах сотен и сотен миллионов вызывает ужас. Да еще мы знаем эту страну, как ту, которая является фартически родиной цыган. Люди образ жизни и ценности которых не вызывают у меня востога, если выражаться относительно корректно.

Но постепенно многие начали присылать хорошие комменты и общий уровень пошел вверх. И продолжая эту тенденцию я хотел бы вспомнить что-то хорошее, связанное с этой и страной и цивилизацией. Конечно же сразу де приходит на ум слова Ивана Антоновича Ефремова о великой и мудрой культуре этой цивилизации. Я также вспоминаю, как  будучи еще совсем ребенком, смотрел вместе с моей мамой трогательные и душещипательные (почти-трагедии) индийские фильмы. Я даже помню некоторые названия этих фильмов. Я должен признаться признаться, что я не очень большой поклонник этой стрвны сейчас. И не очень люблю их фильмы сейчас. Но я признаю их успехи и желаю им преодолеть свои проблеммы. 

Кроме того, поскольку математика это моя первая любовь, а любой человек первую любовь помнит всегда, я вспомнил этого индийского гения. Рамануджан. Молодой парень, который был практичести самоучкой и самостоятельно открыл множество уже открытых формул Эйлера (русского математика). Но он на этом не остановиося и открыл еще множество новых неизвестных ранее формул. Здесь, сегодня, не будет много цитат и афоризмов в обычном смысле. Мы будем говорить о математике. 

Мой учитель математики, в то время, когда я был в очень нежном возрасте впервые ркссказал мне об этом человеке, который достоин нобелевки намного больге, чем некто по имени Альберт.

(Да. Я знаю, что нобелевку не дают в математике, пэтому Леонид Конторович получил ее в экономике, в 1975 году. Тогда синус был меньше или равен одному и намного меньше лжи в мире было, но уже было и уже началось :)

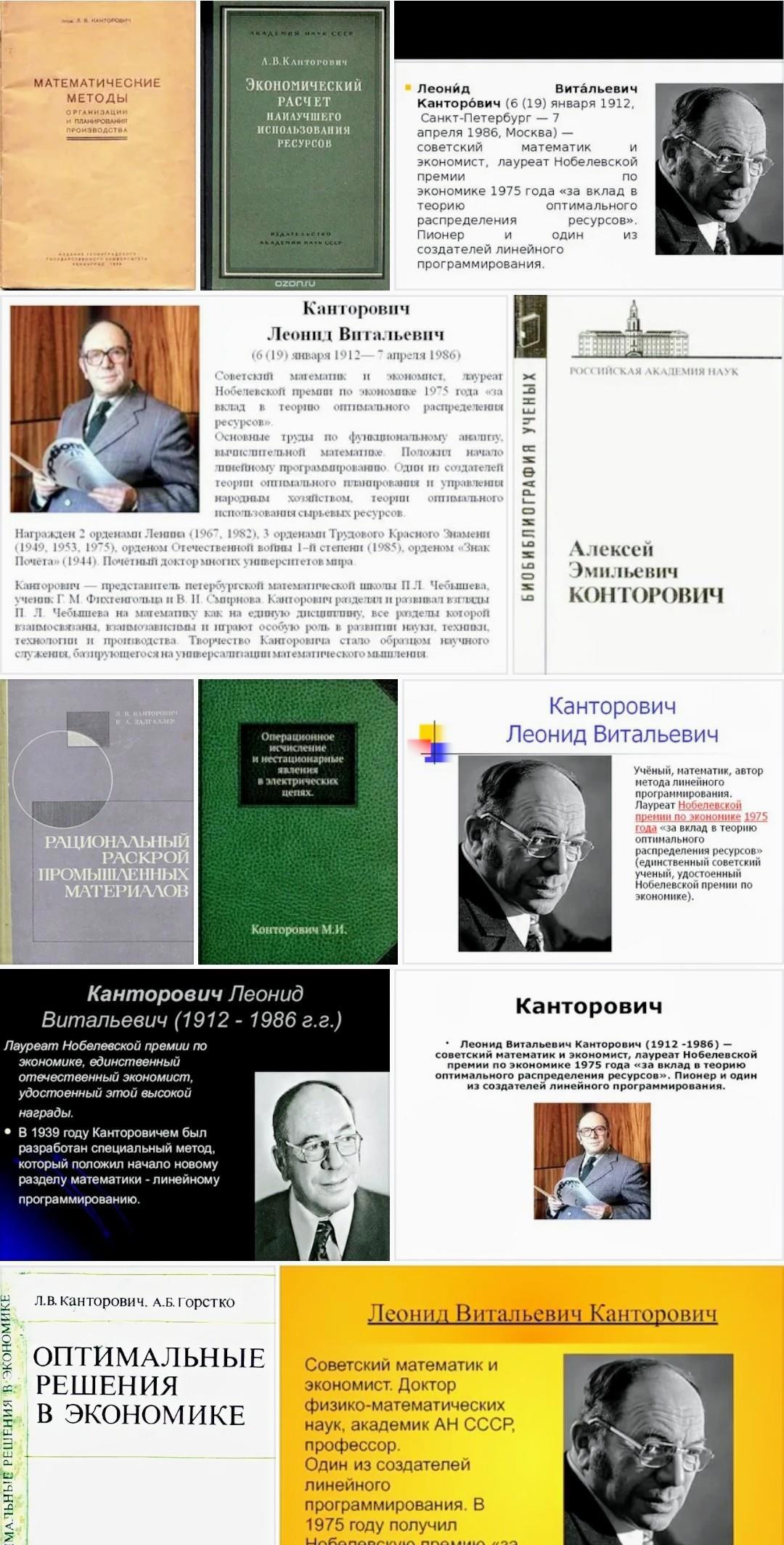
Но не будем забираться в чисто математические дебри. 

Высказывания Великих людей. Рамануджан (Сринива́са Рамануджан Айенго́р)

Сринива́са Рамануджан Айенго́р (произношение (инф.); там. ஸ்ரீனிவாஸ ராமானுஜன் ஐயங்கார்; англ. Srīnivāsa Rāmānujan Iyengar; 22 декабря 1887 — 26 апреля 1920) — индийский математик.

Дата смерти:  26 апреля 1920 (32 года)

Дата рождения: 22 декабря 1887Научная сфера: математика

***

Около 75 лет назад гениальный индийский математик придумал невероятно эффективные способы вычисления числа p. Созданные сейчас на той же основе алгоритмы для компьютеров позволяют найти миллионы десятичных знаков числа p

Число ; – отношение длины окружности к её диаметру – в 1987 г. было вычислено с беспрецедентной точностью: более ста миллионов десятичных знаков. Этот год ознаменовался также столетием со дня рождения Сринивасы Рамануджана – гениального индийского математика, который б;льшую часть своей недолгой и загадочной жизни был оторван от остального математического мира. Эти два события тесно связаны между собой, ибо самые недавние методы вычисления ; предвосхищены Рамануджаном, хотя для их реализации пришлось подождать, пока будут разработаны (многими специалистами, в том числе нами) эффективные алгоритмы, новейшие суперкомпьютеры и нетрадиционные методы умножения чисел.  

(ДЖОНАТАН М. БОРВЕЙН, ПИТЕР Б. БОРВЕЙН)

N.B. Далее выдержки из В. Перепелкина.

Фигура Рамануджана как математика тем более удивительна, что его формальное образование было весьма ограниченным. Он родился 22 декабря 1887 г. в небогатой семье касты браминов в местечке Эрод на юге Индии и вырос в городке Кумбаконаме, где его отец служил бухгалтером в небольшой текстильной лавке. Его математический талант был замечен очень рано, и в возрасте 7 лет он получил право на стипендию для учёбы в средней школе Кумбаконама. Он поражал одноклассников тем, что помнил наизусть сложные математические формулы и много знаков числа ;.

В 12 лет Рамануджан изучил обширный труд С. Л. Лоуни «Плоская тригонометрия», включая рассмотренные там суммы и произведения бесконечных последовательностей, которым суждено было занять важное место в его последующих работах. Через три года Рамануджан достал книгу «Сборник элементарных результатов чистой математики» (Synopsis of Elementary Results in Pure Mathematics), содержащий свыше 6000 теорем (большей частью без доказательств) и составленный преподавателем Кембриджского университета Дж. Ш. Карром. Две эти книги и стали основой математической подготовки Рамануджана.

В 1903 г. Рамануджан был принят в местный колледж (входивший в состав Мадрасского университета. – Перев.). Однако поглощённый своими математическими изысканиями в ущерб всему остальному, он провалился на экзаменах; то же самое повторилось четыре года спустя в другом колледже в Мадрасе. После женитьбы в 1909 г. Рамануджан на время оставил своё увлечение и попробовал найти работу. К счастью, в 1910 г. по pекомендации многих сочувствующих Рамануджану индийских математиков на него обратил внимание богатый любитель и покровитель математики Р. Рамачандра Рао. Под впечатлением открытий, законспектированных Рамануджаном в его «Тетрадях», Рамачандра Рао предоставил ему ежемесячное пособие.

В 1912 г., желая всё-таки иметь работу, Рамануджан устроился бухгалтером в Трест мадрасского порта, который возглавлял английский инженер Френсис Спринг. Вместе с основателем Индийского математического общества В. Рамасвами Айяром они уговорили Рамануджана сообщить свои результаты трём известным английским математикам. Двое из них, по-видимому, не отозвались.

Г. Г. Харди

Третьим был Г. Г. Харди из Кембриджского университета, признанный теперь самым выдающимся английским математиком того времени. 

Харди, привыкший к письмам от всякого рода «умников», получив послание Рамануджана 16 января 1913 г., сначала был склонен его проигнорировать. Однако вечером того же дня он решил вместе с коллегой и близким другом Джоном И. Литлвудом поломать голову над списком из 120 формул и теорем, которые Рамануджан приложил к своему письму. Через несколько часов они «вынесли приговор» – перед ними работа не маньяка, а гения. (По составленной Харди позднее «шкале чистого таланта» для математиков Рамануджан получил 100 баллов, Литлвуд – 30, а себе Харди поставил 25. Немецкий математик Давид Гильберт, самая влиятельная фигура в математике того времени, заслужил только 80.) Этот эпизод и то, что за ним последовало, по словам Харди, было единственным романтическим событием его жизни.

Он писал, что некоторые формулы Рамануджана его совершенно ошеломили, но тем не менее «они, несомненно, верны, ибо если бы они были неверны, ни у кого не хватило бы воображения их выдумать».В течение следующих пяти лет Харди и Рамануджан работали совместно в Тринити-Колледже Кембриджского университета. Сочетание блестящего мастерства Харди-аналитика и фантастической интуиции Рамануджана привело к необычайно плодотворному сотрудничеству. Они опубликовали серию основополагающих работ о свойствах различных теоретико-числовых функций, открывавших путь для ответа на вопросы типа: каково наиболее вероятное число простых делителей у данного целого числа? Сколькими способами можно выразить натуральное число в виде суммы меньших натуральных чисел?В 1917 г. Рамануджан стал действительным членом Лондонского королевского общества и профессором Кембриджского университета. Впервые индиец был удостоен того и другого звания. Слава его росла, однако здоровье резко ухудшилось. В военное время, когда в Великобритании остро ощущалась нехватка продовольствия, трудно было придерживаться вегетарианской диеты, которую он строго соблюдал. Рамануджан не раз попадал в больницу, но поток его новых результатов не иссякал. В 1919 г., когда война закончилась и путешествия за границу снова стали безопасными, он вернулся в Индию. Ставший кумиром молодых индийских интеллектуалов 32-летний Рамануджан умер 26 апреля 1920 г., как тогда думали, от туберкулёза, но, скорее, как считают теперь, от острого недостатка витаминов.***

Высказывания Рамануджана Сриниваса:

Для меня уравнение не имеет никакого смысла, если не выражает мысль Бога.  

(Сриниваса Рамануджан)

***

Некоторые Высказывние о математике:

***

"Математика — это искусство называть разные вещи одним и тем же именем".                  

(Жюль Анри Пуанкаре)  это именно он настоящий автор Теории относительности

"Пристальное, глубокое изучение природы есть источник самых плодотворных открытий математики 

(Жан Фурье)

"Добрый христианин должен опасаться математиков и всех ложно пророчествующих. Есть опасность, что математики вступили в сговор с дьяволом, чтобы очернить Бога и ввергнуть человека в ад."

(Блаженный Августин)

Бог существует — ибо математика непротиворечива, но существует и дьявол — ибо мы не можем доказать ее непротиворечивость. (Андре Вейль)

Все, что познается, имеет число, ибо невозможно ни понять ничего, ни познать без него.  (Пифагор)Современная наука очень насыщена математикой, и лишь немногочисленные специалисты достаточно владеют последней, чтобы разобраться в ,фундаментальной физике,., Кто-то сказал мне, что каждое уравнение, включённое в ,научно-популярную, книгу, уменьшает число её покупателей вдвое. — Обобщение цитаты: в оригинале имелась в виду именно его книга («Кто-то сказал мне, что каждое уравнение, включённое мной в эту книгу, уменьшит доход от её продаж вдвое.»), но в данном контексте пример вполне распространяется на научно-популярную литературу по физике вообще.   (Стивен Уильям Хокинг)

Поэт должен видеть то, чего не видят другие. И это же должен и математик.  

(Софья Ковалевская)

В любой науке столько истины, сколько в ней математики. — Парафраз Канта: «В каждом отделе естествознания есть лишь столько настоящей науки, сколько в нем математики» (Метафизические основы естествознания, 1786 г.).  (Иммануил Кант)

Легко на самом деле выйти из дома в лес математики, но лишь немногие смогли оттуда вернуться.  (Гуго Штейнгауз)

Все искусства тяготеют к музыке, все науки – к математике.  (Джордж Сантаяна)

Если тебе трудно сразу понять всю бесконечность, постарайся понять ее хотя бы наполовину. (Славомир Врублевский)

Математика — это язык!  (Дж. Гиббс)

***

Некоторые факты о числе пи:

***

Число PI состоит из бесконечного набор цифр. Оно иррационально, это значит, что наборы цифр в нём никогда не начнут повторяться. Пока что математики не доказали, что внутри числа PI можно найти вообще любой конечный набор цифр, но всё указывает на то, что так и есть. Внутри числа PI есть дата вашего рождения, есть номер вашего телефона, все данные ваших детей и родителей, ваши счета в банках и прочее, прочее и прочее. 

Если перевести число PI в двоичную форму, то можно найти в числе PI и текстовую информацию. Получается, что если внутри PI можно найти любую последовательность чисел, то там также содержится и любой мыслимый текст, в том числе и этот пост, и полное собрание всей мировой литературы и ваши утренние мысли и рецепт лекарства от рака. Нужно только перевести число PI в двоичную форму, перекодировать в текст и указать позицию. Например, с 1238889242142411231253464564564123333312 1556687862113-й позиции находится текст сожженного тома мёртвых душ, а с 82785472390450234723845532-й ваша биография. Все тайны вселенной внутри одного числа! Нужно только знать позицию. 

Например фраза "helpme" нашлось в числе PI на позиции 2773955512. 

Интересно: "Что если это настоящий крик о помощи?". Если в числе PI действительно есть вся информация о вселенной, то и крики о помощи тоже должны быть. Но кто просит о помощи и о чём?

В процессе вычислений этих самых знаков было открыто множество разных научных методов и целых наук. Но самое главное – в десятичной части числа пи нет повторений, как в обычной периодической дроби, а число знаков после запятой у него – бесконечно. На сегодняшний день проверено, что в 500 млрд. знаков числа пи повторений действительно нет. Есть основания полагать, что их нет вообще.

Поскольку в последовательности знаков числа пи нет повторений – это значит, что последовательность знаков числа пи подчиняется теории хаоса, точнее, число пи – это и есть хаос, записанный цифрами. Более того, при желании, можно этот хаос представить графически, и есть предположение, что этот Хаос разумен. В 1965-м году американский математик М. Улэм, сидя на одном скучном собрании, от нечего делать начал писать на клетчатой бумаге цифры, входящие в число пи. Поставив в центре 3 и двигаясь по спирали против часовой стрелки, он выписывал 1, 4, 1, 5, 9, 2, 6, 5 и прочие цифры после запятой. Попутно он обводил все простые числа кружками. Каково же было его удивление и ужас, когда кружки стали выстраиваться вдоль прямых!

В десятичном хвосте числа пи можно отыскать любую задуманную последовательность цифр. Любая последовательность цифр в десятичных знаках числа пи рано или поздно найдется. Любая!

А это опять-таки означает, что там содержится не только вся мировая литература, которая уже написана (в частности и те книги, которые сгорели и т.д.), но и все книги, которые еще БУДУТ написаны. В том числе и Ваши статьи на сайтах.  Получается, что это число (единственное разумное число во Вселенной!) и управляет нашим миром. Надо только рассмотреть побольше знаков, найти нужный участок и расшифровать его. Это чем-то сродни парадоксу со стадом шимпанзе, долбящем по клавиатуре. При достаточно долгом (можно даже оценить это время) эксперименте они напечатают все пьесы Шекспира.

***

N.B. Числу Пи посвящено множество фантастических рассказов. В одном из тауих рассказов предсказан конец всех времен, когда число пи начнет повторять числа.

***

N.B. Смотрите ссылки на мои ранние блоги и статьи о магических числах в конце статьи.

***

N.B. Друзья прислали в догонку:

***

N.B. Ссылки на другие похожие статьи и блоги:

Ссылки о магических числах и математике:

ТЕМА Математика, Физика, Точные Науки

https://author.today/reader/174567/1428052

***

Ccылка на фильм о Рамануджане:

Человек, который познал бесконечность

https://www.kinopoisk.ru/film/841613/

***

Индия, что она собой представляет? Неизвестная Известная Страна:

Прекрасное Далеко, Часть 43
Том: https://author.today/work/198384

Блог: https://author.today/post/279582

***

ТЕМА Известные Личности и их Высказывания и Работы

https://author.today/reader/174567/1427514

***

Полностью прочитать статьи о пи вы можете по этим ссылкам :

https://zengarden.in/blogi/komu-pi-a-komu-xu.html

***

https://mozgosteb-livejournal-com.turbopages.org/mozgosteb.livejournal.com/s/52311.html

P.S. В статье использованы материалы личного архива (>100 К фоток), с сайтов Wiki, В. Перепелкин (proza.ru), Частичный пкревод фрагментов S. Wolfram "Who Was Ramanujan?, а также фрагменты статьи В. Перепекина, mozgosteb (жж), zengarden.ru,

***
P.P.S. Ссылки на все книги серии находятся в каталоге "Прекрасное Далеко, Хронология, Тематики, Индекс" на сайте "Author Today":
Том: https://author.today/work/174567