Математика, Учителя, лист Мёбиуса, бутылка Клейна, Топология и сферический конь в вакууме

******

Статья

******

Пример графики тополога профессора Фоменко

Математика, Учителя, лист Мёбиуса, бутылка Клейна, Топология и сферический конь в вакууме

...Лента Мёбиуса уже много лет озадачивает математиков...

N.B. Я очень много занимался математикой в детстве. 

Мой отец прививал мне любовь к ней и повторял, что это самая главная наука. Я участвовал во множестве олимпиад разного уровня, включая всесоюзный уровень, (и всегда довольно успешно). 

Я искренне и безоговорочно полюбил математику и даже учился в математическом классе и рассказывал уже о своём любимом учителе математики, Александре Кузмиче Гусеве. Он был истинным гением и от педагогики и от математики. Мы всегда это подозревали, но понял я это только через много лет :(

Трое из этих четверых людей входят в очень важное и трогательное для меня понятие "мои учителя".  

Великолепный математик, Александр Кузьмич Гусев - крайне левый. Рядом с ним Дмитрий Валерьянович Селянин - другой мой учитель,  по черчению и рисованию. Кстати, и тот и другой прошли всю войну и были на ней во фронтовой разведке. Далее историк - Соломон Борисович. И тоже фронтовик. Последний на этой фотографии,  к сожаленью мне не знаком. 

До сих пор решение математических, логических и других задач приносит мне истинное удовольствие. 

Но. Я не люблю торопиться. Я люблю получать от этого удовольствие. ЛОЛ. 

Тайна Мебиуса разгадана с помощью
Математики спустя 5 десятилетий. 

N.B. Под "тайной" здесь подразумевается следующее : 

Каким должен быть минимальный размер этой полоски бумаги, чтобы получилась лента Мебиуса.

*****

N.B. Это перевод статьи Др. Альфреда Капринети с моими дополнениями и расширениеми. (Ссылка на оригинал статьи а конце).

N.B. Впервые о листе Мёбиуса и бутылке Клейна я услышал в школе и сразу же заинтересовался топологией. Естественно я также начал интересоватья работами прфессора Фоменко. Но это было в основном из-за его графических работ. 

Здесь же я уже делал несколько публикаций и о Мёбиусе и о бутылке Клейна и о Фоменко, и о много ещё чем, например "магических" числах математики, геометрии невозможного Ешера (и не только), Иллюзии и Фракталах... :)

******

N.B. Для начала вспомним, что же такое лист Мебиуса, бутылка Клейна и топология ... :)

******

Ле́нта Мёбиуса (лист Мёбиуса, петля́ Мёбиуса) — топологический объект, простейшая неориентируемая поверхность с краем, односторонняя при вложении в обычное трёхмерное евклидово пространство  {R} ^{3}.

Римская мозаика III века нашей эры с изображением кольца, свернутого как лента Мёбиуса, мюнхенская Глиптотека

Считается, что лента Мёбиуса была открыта независимо немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858 году, хотя похожая структура изображена на римской мозаике III века нашей эры.

Модель ленты Мёбиуса можно легко сделать: надо взять достаточно длинную бумажную полоску и склеить противоположные концы полоски в кольцо, предварительно перевернув один из них. В трёхмерном евклидовом пространстве существуют два типа полос Мёбиуса в зависимости от направления закручивания: правые и левые.

Эйлерова характеристика листа Мёбиуса равна нулю.

******

Что будет, если ленту Мёбиуса разрезать вдоль?

Разрезание ленты Мёбиуса по линии, которая отстоит от краёв на треть ширины.

Если разрезать ленту Мёбиуса, отступая от края приблизительно на треть её ширины, то получаются две ленты, одна — более короткая лента Мёбиуса, другая — длинная лента с двумя полуоборотами

******

Если разрезать ленту вдоль по линии, равноудалённой от краёв, вместо двух лент Мёбиуса получится одна длинная двусторонняя (закрученная на полный оборот) лента. Это свойство ленты Мёбиуса используется в старинном фокусе под названием «афганские ленты» (англ. The Afghan Bands) с 1904 года, его также описывают Норберт Винер в книге I Am a Mathematician (1956) и Мартин Гарднер в книге Mathematics, Magic and Mystery (1956), последний также утверждает, что самая ранняя ссылка на использование ленты Мёбиуса для фокусов относится к 1882 году. Если получившуюся ленту разрезать вдоль посередине, получаются две такие ленты, намотанные друг на друга.

Тополо́гия — раздел математики, который является разновидностью геометрии, посвященной изучению качественных свойств геометрических фигур, не зависящих от расстояний, величин углов, площадей и объёмов.

Слово «топология» происходит от сочетания двух древнегреческих существительных: τόπος — место и λόγος — слово, учение. Буквально оно означает изучение места (пространства) или локальное исследование. Таким образом, топология занимается определением того, что такое пространство и каковы его свойства.

Топология берёт своё начало с изучения некоторых геометрических задач. Различные источники указывают на первые топологические по духу результаты в работах Лейбница и Эйлера.

Приблизительно с 1925 по 1975 годы топология являлась одной из самых бурно развивающихся отраслей математики.

Общая топология зародилась в конце XIX века — и оформилась в самостоятельную математическую дисциплину в начале XX века. Основополагающие работы принадлежат: Хаусдорфу, Пуанкаре (цикл статей Analysis situs), Александрову, Урысону, Брауэру.

Топологическая эквивалентность коровы (без дырок) и шара.

В отличие от геометрии, эквивалентными в топологии, по определению, считаются те фигуры, которые получаются друг из друга произвольной обратимой непрерывной деформацией. Такие деформации называются гомеоморфизмами. Например, сглаживая углы треугольника, его можно деформировать в круг, а затем, заостряя края круга, — в пятиугольник или любой другой выпуклый многоугольник, поэтому с точки зрения топологии все эти фигуры эквивалентны. Кроме того, кружка с ручкой и бублик гомеоморфны. Напротив, бублик и шар, а также кольцо и круг по некоторым причинам не гомеоморфны.

N.B. Здесь все сразу вспоминаем сферического коня в вакууме. ЛОЛ. 

*

Это шутка конечно.  ЛОЛ. 

Все дело в максимально короткой полоске, которую вы можете сделать.
Доктор Альфредо Карпинети
Старший штатный писатель и космический корреспондент 16 октября 2023 г.

Полоски Мебиуса - это забавные геометрические фигуры, у которых есть только одна сторона. Возьмите полоску бумаги – у нее
есть лицевая и оборотная стороны. Теперь скрутите его и склейте два коротких края вместе. Внезапно не остается
ни фронта, ни спины. Вы могли бы провести линию по всей его поверхности, не отрывая
карандаша от бумаги. Сорок шесть лет назад математики предложили минимальный размер
такой полосы, но они не смогли это доказать. Теперь, наконец, кто-то это сделал.
С момента создания ленты Августом Фердинандом Мебиусом и Иоганном Бенедиктом Листингом
простота ее создания и визуализации должна была быть сбалансирована с математическими
сложностями такой формы. 

Неудивительно, что в 1977 году Чарльз Сидни Уивер и Бенджамин Риглер Халперн создали гипотезу Халперна-Уивера, в которой говорилось о минимальном
соотношении между шириной полосы и ее длиной. Они предположили, что для полосы
шириной 1 сантиметр (0,39 дюйма) длина должна была составлять по меньшей мере квадратный корень из 3
сантиметров (около 1,73 сантиметра или 0,68 дюйма).
Для гладких полос Мебиуса, которые “встроены”, то есть не пересекаются друг с
другом, гипотеза не имела решения.
Математик из Университета Брауна Ричард Эван Шварц предложил в 2020 году, что если полоса может проходить сама по себе, то решить эту проблему гораздо проще
, но он допустил ошибку. В статье, опубликованной в качестве препринта – это означает, что она еще
не прошла экспертную оценку, – Шварц исправил ошибку и нашел правильное решение для
гипотезы.
Решение вытекает из леммы, приведенной в его предыдущей статье. Важнейшая концепция заключается в том, что на
поверхности полос Мебиуса существуют прямые линии, проходящие через каждую точку и заканчивающиеся на
границах. Чтобы доказать первую часть леммы, ему нужно было доказать, что существуют
перпендикулярные линии к этим прямым, существующим в одной плоскости. И он это сделал.

“Вовсе не очевидно, что эти вещи существуют”, - сказал Шварц изданию Scientific American.

Следующим шагом было нарезать полоски Мебиуса и понять, какие формы они
образуют. Идея состояла в том, чтобы упростить задачу, выровняв полосу по плоскости. В
оригинальной статье Шварц думал, что нарезанная полоска будет выглядеть как параллелограмм, но
оказалось, что это другой четырехугольник – трапеция.

“Исправленный расчет дал мне число, которое было предположением”, - сказал он. “Я был
ошеломлен... Следующие три дня я почти не спал, просто записывал это”.   (Шварц)

******

N.B. Другие, очень интересные топологические объекты (очень малая их часть. (Очень кратко и не все здесь о топологи  :)

Бутылка Клейна (или бутылка Кляйна]) — неориентируемая (односторонняя) поверхность, описана в 1881 году немецким математиком Феликсом Клейном.

Тесно связана с лентой Мёбиуса и проективной плоскостью. 

Название, по-видимому, происходит от схожести написания слов нем. Fläche (поверхность) и нем. Flasche (бутылка).

*******

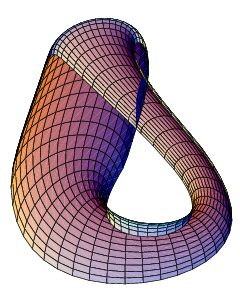При рассечении бутылки Клейна получается лента Мёбиуса

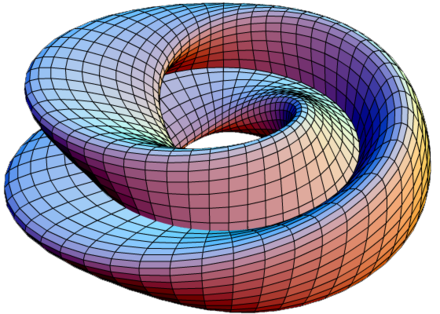Реализация бутылки Клейна в виде восьмёрки

*******

Гомеоморфи́зм — непрерывное обратимое преобразование пространства. Является центральным понятием топологии.

*******

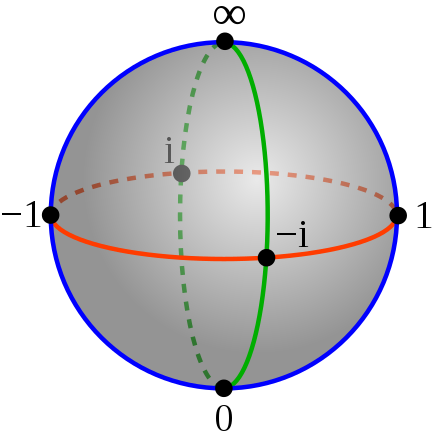
Сфе́ра Ри́мана — наглядное изображение множества  в виде сферы, подобно тому, как множество действительных чисел изображают в виде прямой и как множество комплексных чисел изображает в виде плоскости. По этой причине термин «сфера Римана» часто используется как синоним к термину «множество комплексных чисел, дополненных бесконечно удалённой точкой», наряду с термином «расширенная комплексная плоскость».

******

N.B. Видео по теме :

https://youtu.be/QJC27E9bvqU

******

https://youtu.be/QwSWy9TsbRA

******

******

N.B. Друзья прислали вдогонку:

******

******

******

*******

***