Math, Мёбиус, Клейн, #2, Теория Пуанкаре-Перельмана и графика Тополога Академика Фоменко

*****

N.B. Эта публикация у нас совместная с моим другом, АТ автором и со-редактором : 

Schtern

******

Статья

******

Math, Мёбиус, Клейн, #2, Теория Пуанкаре-Перельмана и графика Тополога Академика Фоменко

N.B. Недавно я сделал небольш публикацию о Топологии,  точнее о её части, связанной с листом Мёбиуса и бутылкой Клейна. Эта тема меня интересует с самого детства.  ЛОЛ.  

Я неоднократно уже её подымал в своих более ранних публикациях. 

В комментариях у меня завязалась переписка с моим другом,  физиком и АТ автором : Schtern 

... после доказательства гипотезы Пуанкаре  гипотеза бесконечности и формы Вселенной в  виде бесконечно самовыворачивающегося тороида получила новое развитие.  Читал недавно, что одна из целей нового орбитального телескопа будет попытка "разглядеть" ось тора. Спасибо, что подняли такую интересную тему.

(АТ автор   Schtern)

N.B. Вот мы и решили с ним сделать совместный пост о теории Пуанкарэ-Перельмана. 

Но об этом чуть позднее. :)

N.B. В статье большинство иллюстраций - это графика другого талантливого тополога, академика Анатолия Фоменко, которая также покорила меня ещё в детстве. :). О нем я также неоднократно упоминал ранее. 

Анато́лий Тимофе́евич Фоме́нко (род. 13 марта 1945, Сталино, Украинская ССР, СССР) — советский и российский математик, специалист в области многомерного вариационного исчисления, дифференциальной геометрии и топологии, теории групп и алгебр Ли, симплектической и компьютерной геометрии, теории гамильтоновых динамических систем. Академик РАН (1994). Лауреат Государственной премии РФ в области науки и техники. Также известен как художник-график и один из художников-постановщиков мультфильма «Перевал».

N.B. Книга Кира Булычева "Перевал" и одноимённый мультфиьм это тема отдельной публикации в ближайшем будущем

*

*

*

*****

N.B. Прошу заметить, что я никак не отношусь к теории А. Фоменко о "Новой Хронологии". Я её не знаю и не уверен, что хочу знать на этом этапе.

Время покажет. ЛОЛ. 

N.B. Однако вернемся уже к теореме Пункаре-Перльмана.  :)

Всякое односвязное компактное трёхмерное многообразие без края гомеоморфно трёхмерной сфере

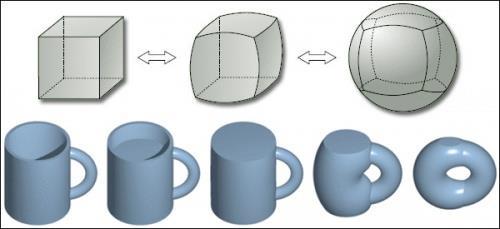
Понятие гомеоморфизма, центральное в топологии. Вообще, топологию часто определяют как «резиновую геометрию», т. е. как науку о свойствах геометрических образов, которые не меняются при плавных деформациях без разрывов и склеек, а точнее, при возможности установить между двумя объектами взаимно-однозначное и взаимно-непрерывное соответствие.

Главную идею проще всего объяснить на классическом примере кружки и бублика. Первую можно превратить во второй непрерывной деформацией.  

(Сергей Дужин,
доктор физ.-мат. наук, старший научный сотрудник Санкт-Петербургского отделения Математического института РАН)

******

В переводе на общедоступный язык, это означает, что любой трёхмерный объект, например, стакан можно преобразовать в шар путём одной только деформации, то есть его не нужно будет ни разрезать, ни склеивать. Иными словами, Пуанкаре предположил, что пространство не трёхмерно, а содержит значительно большее число измерений, а Перельман спустя 100 лет математически это доказал.

 (Просто о сложном, гипотеза Пуанкаре, популярная наука, locnet.ru)

******

1. Имеем воздушный шарик БЕЗ дырки, через которую происходит его надувание - аналог трехмерной сферы.

2. Имеем полое замкнутое тело, например, тарелку, стакан, куб, карандаш, дверь без ручек.

Необходимо доказать, что поверхность этого тела топологически является аналогом сферы, т.е. после проведения определённых деформаций, не вызывающих разрывов данной поверхности, поверхность принимает форму сферы и на этой поверхности действуют те же математические законы, что и на сфере, описываемые теми же функциями в топологии.

Доказательство "для чайников": помещаем тело внутрь нашего воздушного шарика, откачиваем воздух - шарик принимает форму поверхности данного тела, при этом оставаясь шариком, т.е. сферой, для которой по прежнему применимы те же законы, что и для сферы до её деформации. 

 (Просто о сложном, гипотеза Пуанкаре, популярная наука, locnet.ru)

******

Исключительная важность гипотезы, выдвинутой около века назад математиком Пуанкаре, касается трёхмерных структур и является ключевым элементом современных исследований основ мироздания. Загадка эта, по мнению специалистов института Клэя, одна из семи принципиально важных для развития математики будущего.

Дмитрий Кулешов Авиаконструктор, ЧГКшник, джипер., Ulan-Ude

*****

Последним великим достижением чистой математики называют доказательство петербуржцем Григорием Перельманом в 2002–2003 годах гипотезы Пуанкаре, высказанной в 1904 году и гласящей: «всякое связное, односвязное, компактное трехмерное многообразие без края гомеоморфно сфере S3».

(Сергей Дужин,
доктор физ.-мат. наук, старший научный сотрудник Санкт-Петербургского отделения Математического института РАН)

*****

Жюль Анри́ Пуанкаре́ (фр. Jules Henri Poincaré; 29 апреля 1854, Нанси, Франция — 17 июля 1912, Париж, Франция) — французский математик, механик, физик, астроном и философ. Глава Парижской академии наук (1906), член Французской академии (1908)[6] и ещё более 30 академий мира, в том числе иностранный член-корреспондент Петербургской академии наук (1895)

******

Историки причисляют Анри Пуанкаре квеличайшим математикам всех времён. 

Он считается, наряду с Гильбертом, последним математиком-универсалом, учёным, способным охватить все математические результаты своего времени. Его перу принадлежат более 500 статей и книг. «Не будет преувеличением сказать, что не было такой области современной ему математики, „чистой“ или „прикладной“, которую бы он не обогатил замечательными методами и результатами»

******

N.B. Я безмерно уважаю этого человека, Титана мысли,  Анри Пуанкарэ.

"Есть мнение", как говорил бессмертный товарищ Сталин, что Пункарэ является на самом деле автором пресловутый теории  относительности, а не Эйнштейн, который работал в патентном бюро, как раз в отделе открытий. К слову сказать, Эйнштейн, безусловно будучи очень умным человеком, так и не смог до конца жизни избавиться от этой тени. Так ли это на самом деле, сказать трудно. Я как говорится "свечку не держал". ЛОЛ. Однако Пуанкарэ продолжал работать в науке, а вот Эйнштейн вёл жизнь типичную для современного "селебрити". ЛОЛ 

Григо́рий Я́ковлевич Перельма́н (род. 13 июня 1966, Ленинград, СССР) — российский математик, доказавший гипотезу Пуанкаре, которая была нерешённой проблемой около века, а в настоящий момент это единственная решённая математическая проблема из семи задач тысячелетия. 

В начале 1990-х годов приехал в США, где работал в разных университетах.

В 2002—2003 годах опубликовал в Интернете (на сайте arXiv.org) три свои знаменитые статьи, в которых кратко изложил оригинальный метод доказательства гипотезы Пуанкаре.

В декабре 2005 года Перельман ушёл с поста ведущего научного сотрудника лаборатории математической физики, уволился из ПОМИ и практически полностью прервал контакты с коллегами. Свою позицию он объяснил несогласием с организованным математическим сообществом и несправедливостью принимаемых ими решений. 

Проживает в Санкт-Петербурге в Купчино вместе с матерью.

N.B. И в заключение,  ещё немного графики от Анатолия Фоменко.

******

N.B. Видео по теме :

******

https://youtu.be/QwSWy9TsbRA

******

https://youtu.be/QJC27E9bvqU

******

*

***

*

******

N.B. Друзья прислали вдогонку:

https://chronologia.org/art/math/150a191.jpg

Топаз

******

***