Сплайнофобия

Сплайны. 

Линии Безье Графически Транслируемые Кривые ++ 

Впервые познакомился с этим инструментом ещё в школе, когда запускал 3dsMax на своём ламповом пузатом мониторе. Уже позднее, я столкнулся с этим явлением в процессе работы над КПшками. Как и в большинстве случаев, меня с этой тусовкой познакомил богатый(по моим меркам) харизматичный парень. Он показал мне в импортном англоязычном журнальчике кривые, их эротично изгибающиеся выпуклости, их свободу независимость от жестких прямолинейных законов, продиктованных заскорузлыми геометрами древности.

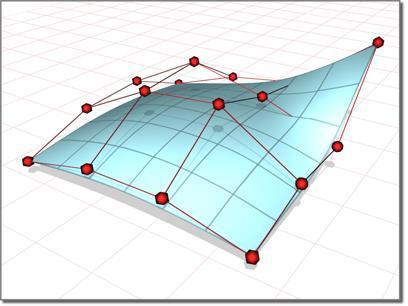
Пока парень отвернулся, я взял другую книжку. Она была сокрыта от простых смертных магическим ореолом иностранного языка, но интуитивно понятные иллюстрации и универсальный язык тела математики, помогли мне преодолеть языковой барьер. Так я впервые задумался о своей геометрической ориентации. 

На тех иллюстрациях великолепные кривые сплетались в страстных взаимодействиях, как тела античных персонажей на картинах Рубенса. Две и более кривые могли совокупиться и образовать единую геометрическую пло(скос)ть, живую и дышащую. Такая криволинейная плоскость уверенно стояла на своих вершинках, но при этом была гибка и воздушна, она изгибала свои полигоны как хотела, легко могла принять форму восьмёрки, совершенно не стесняясь самопересечений, инвертирования нормалей и прочих вольностей, недопустимых в костном обществе прикладных инженеров.

Тогда я закрыл эту книгу. Я не был готов поменять геометрическую ориентацию с традиционной эвклидовой, на новую, неевклидовую, сложную и многообразную. Непозволительно сложную.

Но время шло. Моя эвклидова ориентация только укреплялась. Изучались законы преобразования комплексных чертежей, пересечений точек с плоскостями, свойства классических Платоновых тел. Я стал яростным поборником прямых геометрического ортоганизма. Всё что требовало для понимания больших знаний чем теорема Пифагора или не описывалось рациональными дробями автоматически отвергалось, как ересь. Так продолжалось целый год моей подготовки к вступительным экзаменам.

Но математика всегда будет выше наших представлений о ней. Ей чужды человеческие предрассудки, барьеры непонимания. Она просто смеётся над нами. Не зло. Она умиляется нам, как старшая сестра маленькому братику. В определённый момент я стал замечать щели в заборах, которые держали меня в плену эвклидовости. Разные учителя старательно замазывали пошлость криволинейных поверхностей, маскируя эротическую кривизну пуританскими нарядами из ломанных прямых отрезков. Признаться, я и сам пытался маскировать плавные изгибы множеством острых и тупвх углов, но чем больше я рисовал прямых отрезков, тем больше мне их требовалось. Доходило буквально до абсурда, когжа я считал вручную сотни точек, что должны были описать линию пересечения двых цилиндров построенных в перспективе. 

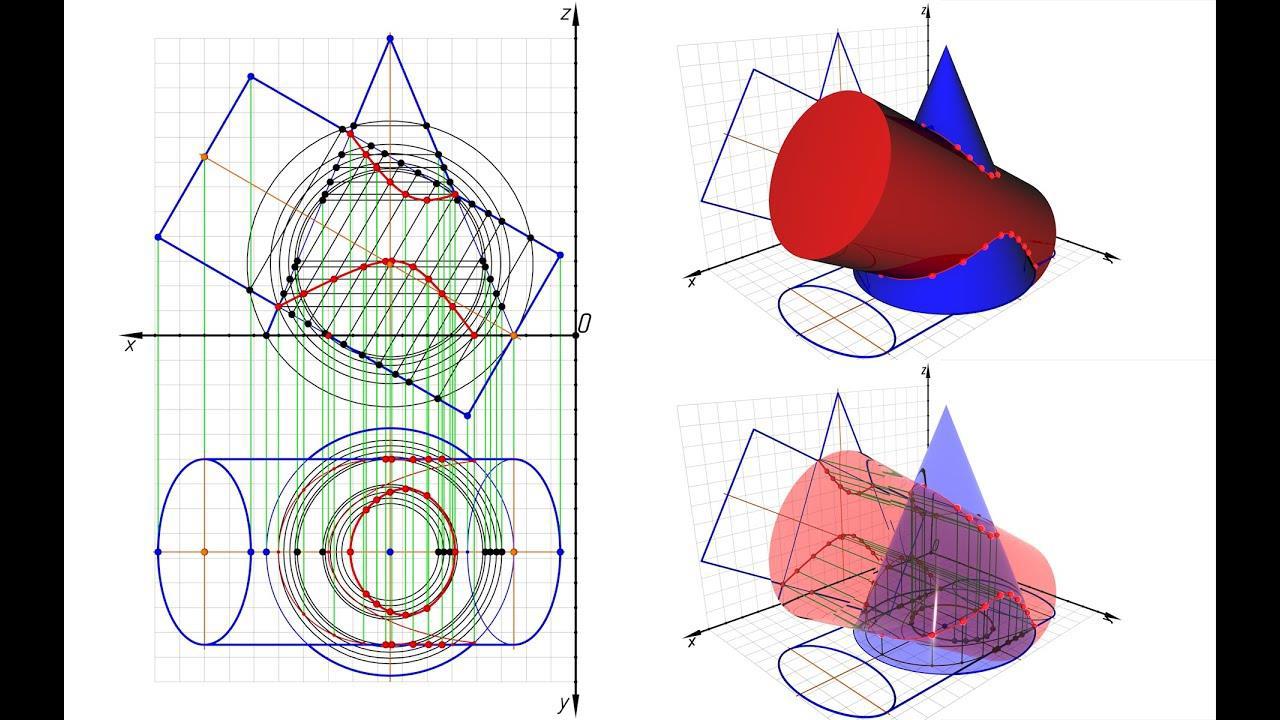
Тогда я понял. Прямых линий не существует. Все линии всегда будут немного кривыми, а идеальная прямая, это по сути та же самая кривая, которая отрицает свою криволинейную сущность. Она буквально кричит на каждом углу о своей прямизне, в тайне боясь в ней усомниться. И чем сильнее её сомнения в собственной прямизне, тем фанатичнее она убеждает себя и других в обратном. Стены ортогональности пали под натиском тригонометрии. 

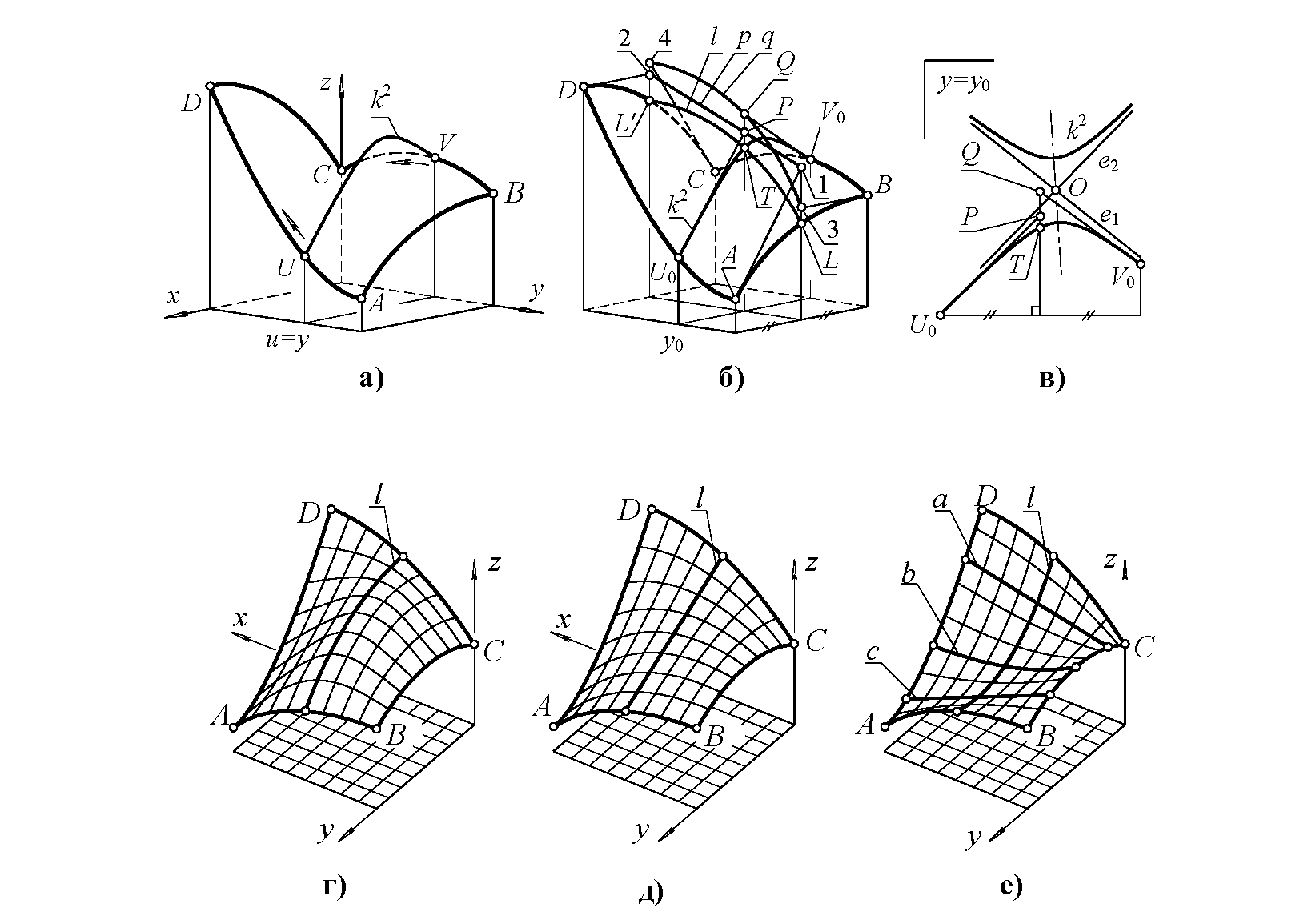
Несметные оргии кривых всевозможных порядков стали наполнять мои эскизы. Я буквально отдался кривизне, и понял что я такой не один. Я понял, что иду по стопам своего кумира Антонио Гауди. Он прошел этот путь за столетие до меня, и составил его карту. Да ещё какую! На этой карте были сотни крестиков, которыми мастер пометил тысячи криволинейных кладов. Это был бесстрашный человек. Он с самого детства отрицал прямизну, совершенно не страшась свирепых церберов ортогональности - инженеров прикладников.

Почему он их не боялся? Нет. С его стороны это не было безрассудством. Они прекрасно знал что делает. Он был настолько умён, что сама физика стала на его защиту. Там где инженеры пытались всё свести к нескольким примитивным и надёжным закономерностям, Гауди просто строил физические модели. Когда инженеры отрицали возможность рассчёта какой-нибудь почти еретической кривизны конструкции, Гауди просто свешивал бусы. Гравитация выстраивала бусинки в устойчивую форму. оставалось очертить её карандашом, и построить из камня. Но он и на этом не останавливался. 

Изобретённые им способы модельного рассчёта устойчивости конструкции были забыты на долгие годы ортоганального до абсурда двадцатого века. Лишь пройдя долгий путь отрицания, набив шишки о жесткое тело физики и материаловедения инженеры были вынуждены построить компьютеры, способные описать то, что сотни лет назад просто понял Гауди, и легко продемонстрировал с помощью ниточек и грузиков. 

Позднее мне удалось побывать и у другого парня. На этот раз инженера прикладника. В его пыльных советских учебниках, ортогональности которых мог позавидовать любой Рейх, я заметил кромолу. На чёрно-белых иллюстрациях я увидел "тёмную сторону" кривизны. Я понял причину, по которой инженеры так отчаянно держались за ортогональность. Имя этой тёмной стороне — Фрактал.

Один смелый учёный решил рассчитать протяженность береговой линии Великобритании. Каково же было его удивление, когда ее протяженность стремилась чуть ли не к длине земного экватора! Он, как как и многие до него, как собственно и я, пытался прикрыть наготу и нескромность кривых линий пуританскими прямыми отрезками. И чем короче и многочисленнее становились отрезки, тем сильнее увеличивалась их суммарная длина. Боюсь даже предположить что он чувствовал в этот момент.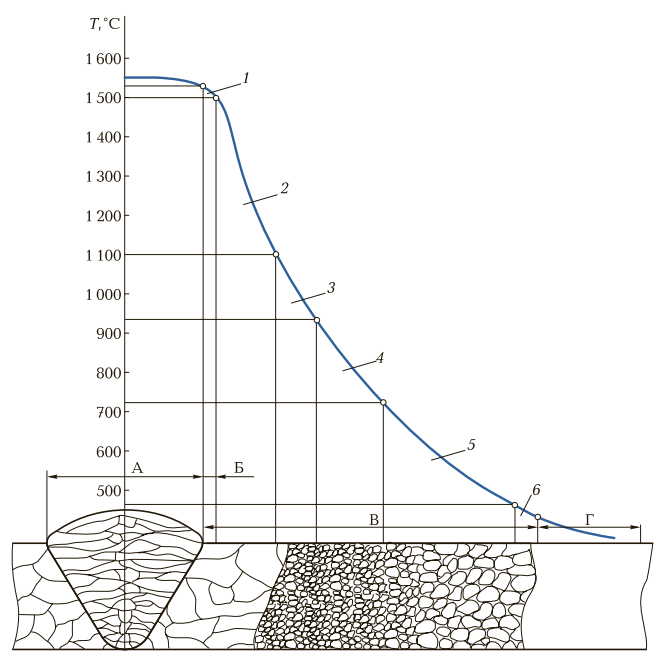 

Но он такой был не один. Химики, сопроматчики и прочие материаловеды, в процессе своей работы регулярно сталкивались с подобными сверх-кривыми линиями. Эти линии и плоскости прятались от непытливого взгляда внутри неоднородных материалов, на графиках упругости полученных эмпирически, в зависимостях прочности от состава испытуемых образцов и методах обработки. Элементарно возьмите разорванный лист бумаги, и посмотрите на рваную кромку через увеличительное стекло.

Если кривые с которыми я сталкивался при пересечении плавных поверхностей были хотя и сложными, но поддающимися описанию. Формула что их описывает могла быть сложной, многозвенной, но она всегда имела ограниченный размер. Фракталам плевать на такие условности. Они просто бесконечно кривые, и всё тут. Преобразования Фурье пока что сдерживают натиск фракталов, но и они скоро падут. Уже трещат.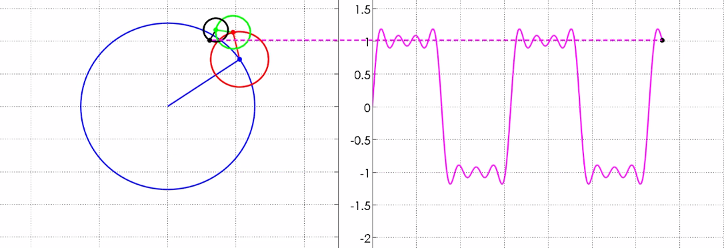

Как же быть? Не то что фракталы, даже обычные кривые ограниченного порядка достаточно сложны для понимания и применения. На помощь пришли двое французов. Обоим инженерам удалось дать бой кривым, оттеснить их на границу погрешности и закрепиться на рубеже на по меньшей мере на сотню лет. Звали этих парней Пьер Безье и  Поль де Кастельжо. Они не только получили достаточно универсальный математический механизм описания причудливости форм, но и создали простой и интуитивный механизм управления ими, знакомый каждому 3дшнику и не только.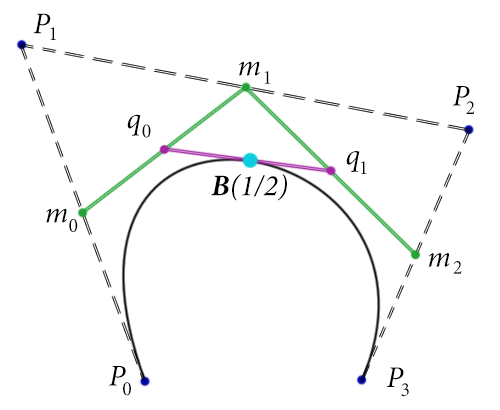

Благодаря их трудам, укрощение кривой стало доступно не только каждому человеку, но и даже компьютеру. Сплаынй стали частью нашей жизни. Они теперь с нами. В каждой детальке промышленного дизайна, в каждой дверной ручке, в каждой пиктограммке и кнопочке закована кривая Безье, и она там надолго.

Но так будет не всегда.

 Живая природа ещё не сказала своего слова. Ждём её в зелёном углу математического ринга.