о соавторстве

Как человек, зело искушённый в соавторствах обоего рода, как-то набросал на коленке... Гуманитариям можно не читать :)

Приводим корректный расчёт изменения соавторской эффективности с течением времени.

Для начала рассмотрим рост литературного качества произведений отдельно взятого  автора. По оси абсцисс будем откладывать время, считая t = 0 за момент создания автором первого текста. Отрезок оси заканчивается с окончанием автором последнего в его жизни текста. Удобно рассматривать отрезки времени в один год, считая, что за год творческой деятельности автор в среднем создаёт один роман. Конечно,  корректнее вместо дискретной оси, ввести непрерывную, в авторских листах или даже тысячах знаков. Однако, это не столь наглядно.

По оси ординат откладываем качество. Качество, по понятным причинам, измеряем в условных единицах, полагая 0 у.е. - унылое говно (УГ), а 100 у.е. - абсолютно гениальный тест (АГ). К сожалению, я не умею строить здесь графики, но, надеюсь, всё будет понятно и так.

В рамках рассматриваемых задач мы можем принять известное упрощение: мастерство автора растёт линейно с годами (количеством созданных авторских листов). Конечно, на деле функция нелинейна, как показывает опыт - зависимость чаще всего логарифмическая, а в редчайших случаях - и экспоненциальная, однако в рамках данного исследования этим фактом можно пренебречь. Тогда мастерство, очевидно,  описывается функцией  f = at+b, где

t - время,

a - коэффициент мастеровитости (обучаемости),

b -  коэффициент исходной литературной одарённости.

Легко видеть, что в случае отсутствия исходной литературной одарённости любой первый текст автора (t=0, b=0) неизбежно оказывается УГ (значение f (tнулевое) = 0).

Напротив, в случае абсолютной гениальности автора (b=100), первый же созданный им текст оказывается АГ -  f(tнулевое) = 100. Заметим, что коэффициент a в этом случае очевидно равен нулю, так как гению обучаться и повышать мастеровитость некуда, и наш график превращается в линию, параллельную оси абсцисс.

Сам же коэффициент мастеровитости а определяет угол наклона прямой роста мастерства к оси абсцисс, следовательно, чем он больше, тем быстрее автор достигнет уровня АГ и тем меньшее количество времени (авторских листов, тысяч знаков) будет им на это затрачено.

На практике, однако, значения b колеблются от 0.1 до 10, а значения а чаще всего таковы, что для достижения уровня АГ  = 100 у.е. качества текста, реальному автору недостаёт от 25 до 250 лет творческой жизни.

Теперь запишем уравнение качества текста для соавторского коллектива из N соавторов. Хорошо известно, что это не может быть простой алгебраической суммой соответствующих f этих авторов, поэтому необходимо введение коэфффициента рождения нового качества (Q). Очевидно, что данный коэффициент также является функцией времени как показывает опыт, для коллектива из двух соавторов он в начале соавторства существенно выше единицы, но с течением времени функция Q стремится к значению Q=1, то есть корректно будет записать её в виде гладкой функции, асимптотически стремящейся с течением времени к значению 1. Расчёт этой функции целесообразно привести отдельно, для простоты же можно пока считать, что Q = const и не зависит от t. Кроме того, следует ввести поправку на авторскую индивидуальность. В соавторстве она, очевидно, будет уменьшать Q как степенная функция в степени, обратной количеству соавторов N.

Итак, основная формула уровня литературного произведения, написанного в соавторстве, Ls в зависимости от времени, выглядит следующим образом:

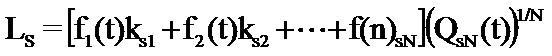
где f1(t), f2(t) и т.д. - количество мастерства н-ного соавтора в момент времени t

Ks1, Ks2 и т.д. - доля соавторского участия (работы над текстом) каждого соавтора (Кs1 + Ks2 + ... Ksn = 1)

Полученная несложная зависимость полезна тем, что на её основе легко рассчитать, за какой период времени коллектив из более одного автора достигнет уровня АГ, равно как и оптимально количество соавторов N.

Благодарю за внимание.