Простые числа.

С университета ЛЭТИ я рассматриваю простые числа. Мне интересно исследовать их расположение. Я пытался разместить статью о них на хабрахабр, однако она не прошла модерацию. Вчера я решил повспоминать тот метод поиска, что я предлагал когда-то давно. Поэтому я решил сегодня вернуться к данной теме.

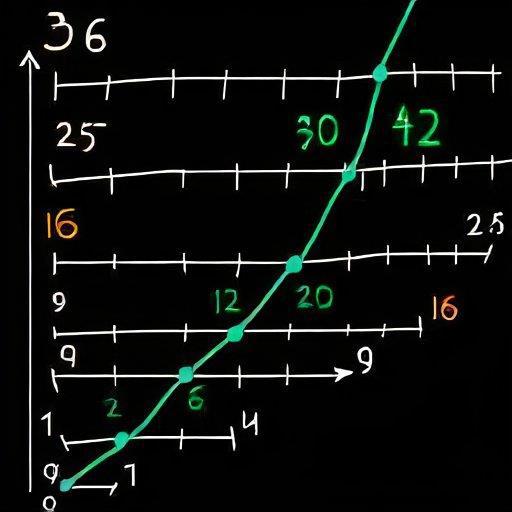
Для поиска простых чисел я решил оттолкнуться тогда от квадрата числа. Если складывать последовательно нечетные числа (1, 3, 5, 7, 9), мы будем получать следующий квадрат числа. - 1, 4, 9, 16, 25...

Также я вывел для поиска парных чисел формулу, напоминающую по своей форме дискриминант. Благодаря ему я нашел линию от-но, которой располагаются простые числа. Вот места, где проходит эта прямая, через ось икс: 0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110. (К числу последовательно прибавляется 2, 4, 6, 8, 10, 12, 14...)

Также интересно, что эта "ось", относительно которой располагаются простые числа, находится на расстоянии корня от квадрата числа. То есть если из 11*11 = 121 - 11 получим 110, а если к 100 прибавить 10 получим то же самое место = 110!

При этом простые числа располагаются достаточно часто симметрично относительно этой точки. На одинаковом расстоянии.

Давайте рассмотрим это подробнее. 

В квадратных скобках место симметрии, а в круглых квадраты. Между ними расположены простые числа.

[(0)] (1) 

(1) [2] 3 (4)

(4) 5 [6] 7 (9)

(9) 11 [12] 13 (16)

(16) 17 19 [20] 23 (25)

(25) 29 [30] 31 (36)

(36) 37 41 [42] 43 47 (49)

(49) 53 [56] 59 61 (64)

(64) 67 71 [72] 73 79 (81)

(81) 83 89 [90] 97 (100)

(100) 101 103 107 [108] 109 113 (121)

Как мы видим из этого примера количество простых чисел между двумя квадратами постепенно увеличивается. Это означает, что между квадратами будет находиться все больше простых чисел.

Таким образом:

Мы можем увидеть следующую особенность: " Количество простых чисел между квадратами чисел постепенно увеличивается." Что позволяет утверждать, что простые числа бесконечно присутствуют на оси.

Я смог обнаружить следующее свойство: " Существует прямая, относительно которой возможно осуществлять поиск простых чисел."

Я предполагаю, что это свойство способно упростить поиск простых чисел. Возможно будет проще искать корни х1, х2. относительно этой прямой.