Про теорию вероятности и людей с опухшим ЧСВ.

Из-за задачки https://author.today/post/522218 разгорелся нешуточный срач. 

Я уже высказывал свои печальные мысли по этому поводу https://author.today/post/522506 

Противоположная сторона тоже высказала, у себя в блоге.

Внимание встречный вопрос:
Чего не хватает Николаю и Евгению для признания своей ошибки, если они трут посты тех, кто просто на нее указали?

Ладно я со своим МПГУ (и пофиг что ведущий педвуз страны), но человеку не смог доказать что он ошибается даже Физмат МГУ! Это какой величины должен быть ЧСВ? с таким вообще ходить можно?

И дала вот такое решение - 

Дано:

6 контейнеров по 2 пирожка каждый. 

в 2х контейнерах по 2 пирожка с яблоком: "яя"

в 3х контейнерах 1 яблоко и 1 малина: ям

в 1м контейнере 2 с малиной: мм

после того как мы в случайно выбранном контейнере взяли в руки один из пирожков, выяснилось что он с яблоком.

Вопрос:

какова вероятность того, что второй пирожок в этом контейнере тоже с яблоком?

Решение:

Изначальный массив выглядит как:

яя, яя, ям, ям, ям, мм

после того как мы в случайно выбранном контейнере взяли в руки один из пирожков и выяснилось что он с яблоком, контейнер с 2мя пирожками с малиной покидает выборку! - тк это точно не он! в итоге у нас один пирожок заявлен как 100% с яблоком и массив выборки теперь выглядит так:

яя, яя, ям, ям, ям

тк нас, по вопросу в задании, интересует ВТОРОЙ пирожок (про первый мы и так знаем что он 100% яблоко), то по 1 яблоку из каждой клетки массива мы можем убрать. тем самым мы получаем массив:

я, я, м, м, м

это обычный простейший линейный массив, в котором мы должны посчитать вероятность (читай процент от общего числа), одного из вариантов. сумма всех вариантов = 5. сумма требуемых вариантов =2. 

соответственно количество нужных вариантов делим на общее количество: 2/5.

Ответ: 2/5

Практически аналогичная задача дана в учебнике - «Введение в теорию вероятностей и ее приложения» том 1

Автор: Феллер. В 

Эту задачу я и решил донести до "физмата МГУ" с компанией.

На что получил ответ - 

После того, как я привел скан из учебника начался цирк -

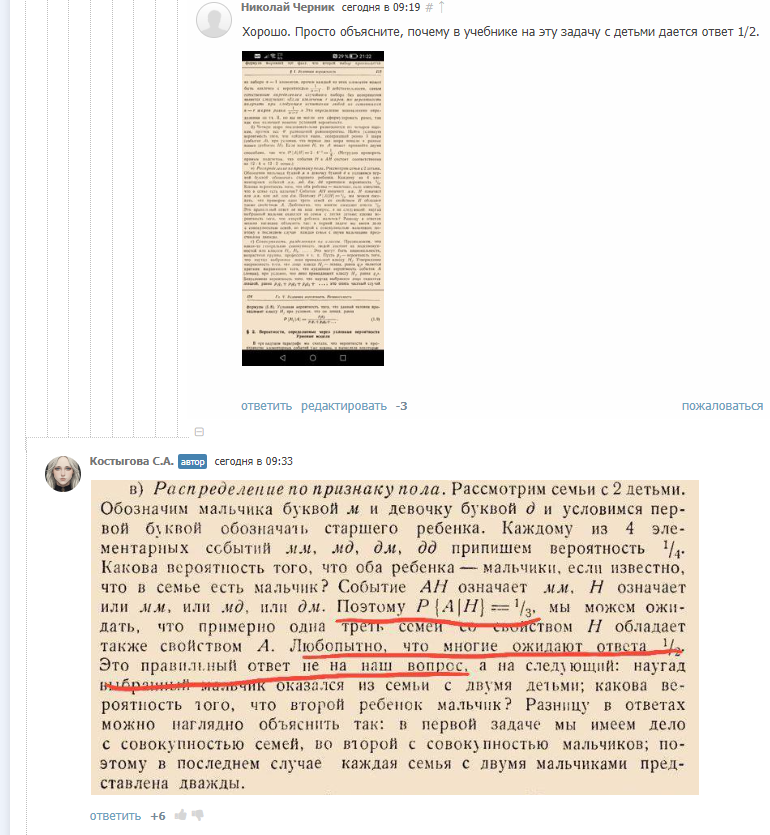
Моё предложение если непонятен учебник посмотреть эту же задачу в википкдии - 

это задача из "детей Смита" или "парадокса мальчика и девочки", одна из.

Из всех семей с двумя детьми, один ребенок выбирается случайным образом, и пол этого ребенка указывается как мальчик. Это даст ответ1/2. [3] [4]

https://en.m.wikipedia.org/wiki/Boy_or_girl_paradox

И там чётко описано, что при случайном выборе вероятность "второй ребенок мальчик" 1/2.

Но нет, цирк продолжился -

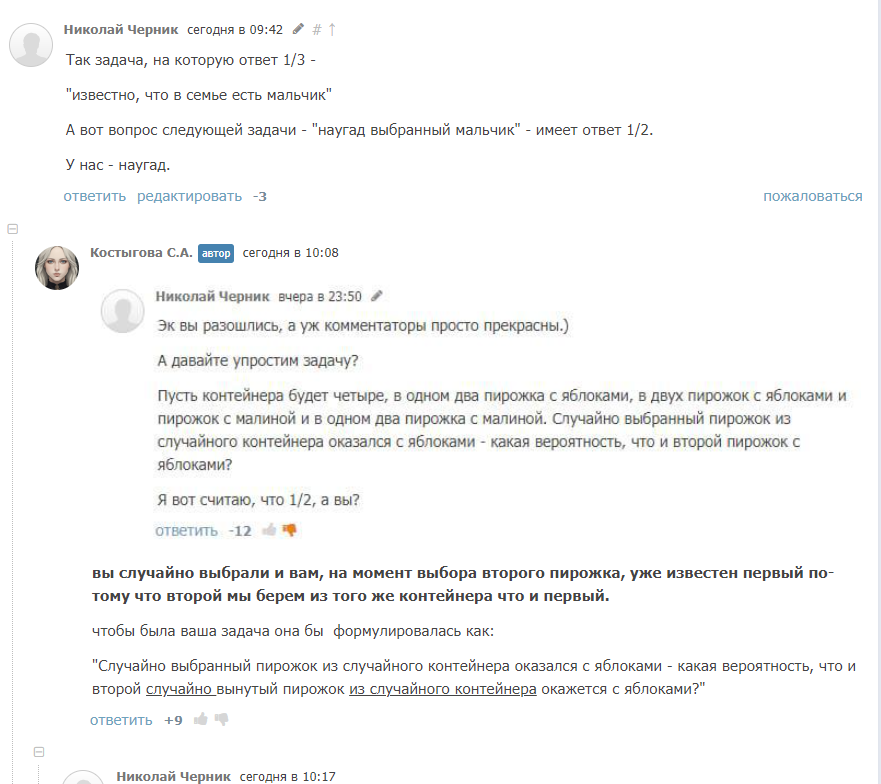
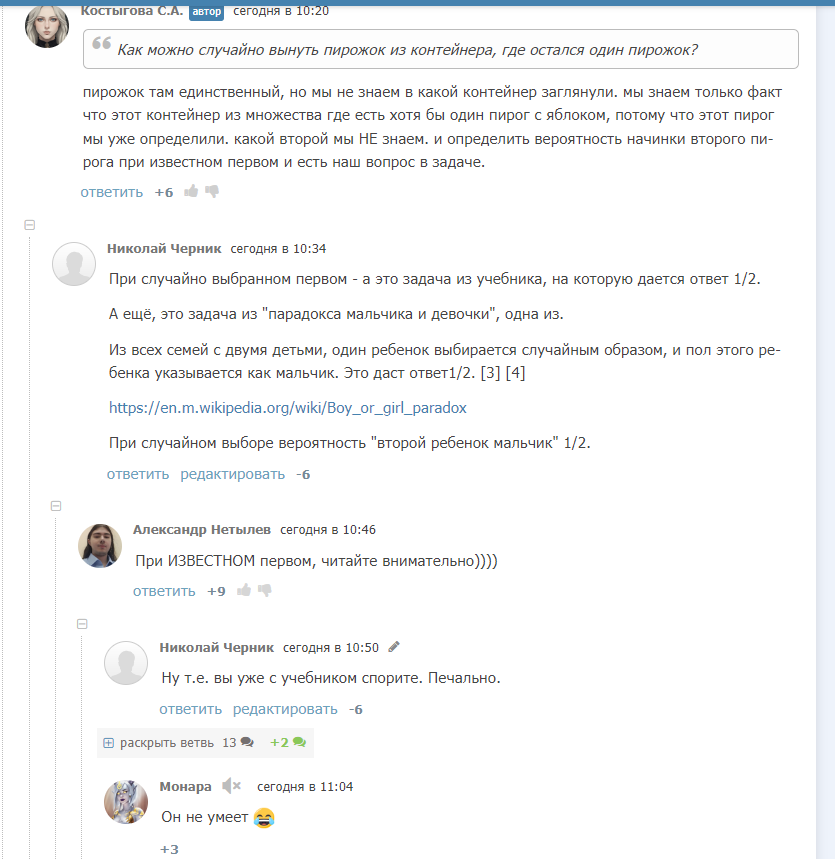
Ну и куда без Табаки, да.)

"Физфак МГУ" упёрся, и извратил понимание учебника немыслимым образом.

Принять, что если объект из группы выбирается случайно, то от вероятности выбрать группу мы переходим к вероятности выбрать объект из группы - эти люди не хотят и не могут.(

После чего непонимайки победно прикрепили сканы из учебника, объявив свою правоту.

В общем, спорить со всей этой компашкой я больше не намерен, и заношу их в список неуподоблюсь.

И о хорошем. В комментах к задачке два человека, сначала не принявшие решение 4/7, проверили его опытным путём и согласились с ним - спасибо вам, вы вернули мне веру в людей.)