Множество Мандельброта : фракталы

В 1975 году Бенуа Мандельброт потряс мир математики открытием фракталов — необычных геометрических структур, которые стали известны широкой публике благодаря ярким компьютерным изображениям. Однако мало кто тогда догадывался, как радикально это открытие изменит наше понимание природы и влияние на многие области науки и технологий.

 Визуальный подход к математике

Мандельброт с раннего возраста обладал уникальной способностью визуально воспринимать сложные структуры окружающего мира. Этот дар помог ему найти альтернативу традиционным математическим методам анализа. В IBM, где он работал, Мандельброт исследовал турбулентные процессы и заметил, что их структура сохраняется независимо от масштаба — будь то за секунду или за день. Эти наблюдения подтолкнули его к идее, что за видимой случайностью скрываются более глубокие закономерности.

Мандельброт вспомнил совет своего дяди, известного математика Шолема Мандельброта, о применении итерационных методов, разработанных ранее Пьером Фату и Гастоном Жюли. В 1980 году, используя мощные компьютеры IBM, Мандельброт смог вычислить и визуализировать результат этих уравнений. Так была обнаружена уникальная форма, впоследствии названная «множеством Мандельброта», которая демонстрировала самоподобие: маленькие детали повторяли основную форму, и это продолжалось бесконечно.

Фракталы в природе

Мандельброт ввел термин «фрактал», чтобы описать эти самоподобные структуры, и в 1982 году опубликовал книгу «Фрактальная геометрия природы». Он показал, что фракталы — это не только абстрактные математические объекты, но и универсальные структуры в природе. Деревья, облака, береговые линии, горы — всё это примеры фракталов, где форма повторяется на разных уровнях, создавая органичную и сложную симметрию.

Природа, как заметил Мандельброт, вовсе не стремится к идеальным формам, которые описываются традиционной геометрией. 

Облака не сферические, горы не конические, а береговые линии вовсе не гладкие. В этих «шероховатостях» и заключается красота фракталов, которые подчеркивают естественный хаос и непредсказуемость окружающего мира.

Применение фракталов

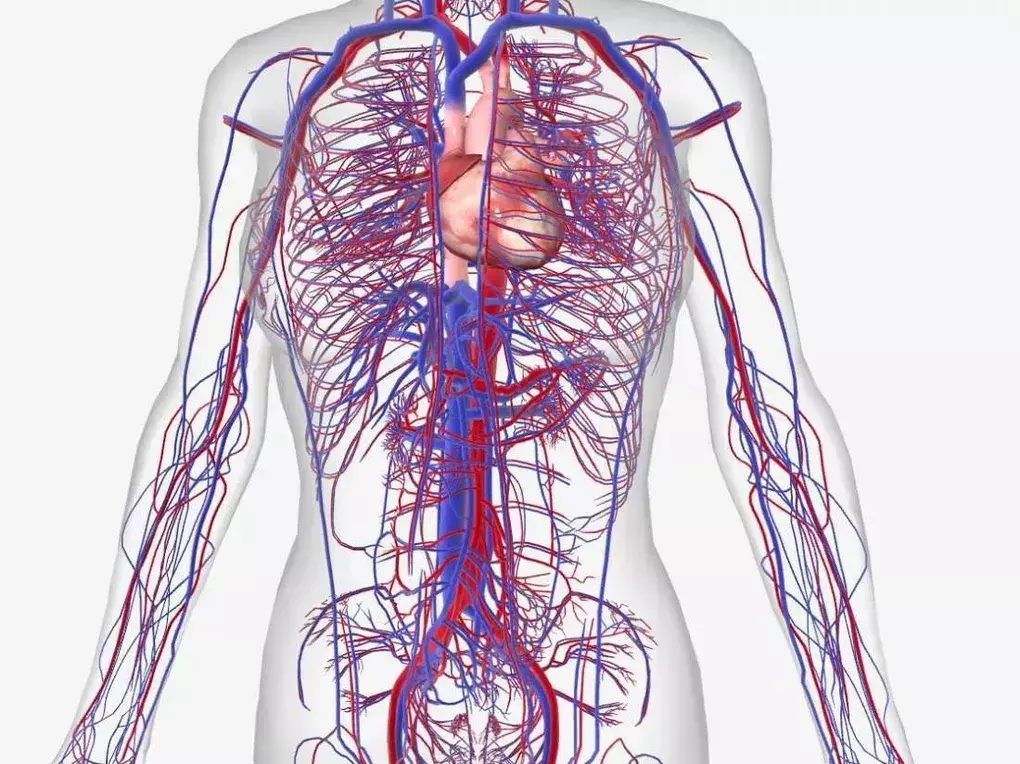
Фрактальная геометрия нашла применение в самых разных областях — от компьютерной графики до медицины и финансов. В IT фракталы используют для создания реалистичных визуализаций и систем сжатия данных. В биологии фрактальные структуры обнаружены в процессах работы организма, таких как распределение крови или сердечный ритм.

Фракталы применяются и в медицине. Например, ученые используют их для диагностики заболеваний почек, анализируя фрактальные структуры кровотока. В финансах фрактальная математика помогает моделировать сложные рыночные колебания, позволяя более точно предсказывать изменения цен.

Наследие Мандельброта

Бенуа Мандельброт оставил глубокий след в науке, предложив новую парадигму восприятия мира. Его открытия помогли понять, что хаотические явления могут подчиняться строгим математическим правилам. Сегодня фракталы остаются ключевой концепцией в понимании сложных систем, а работы Мандельброта продолжают вдохновлять ученых, исследующих природу, финансы и технологии.

Почему фракталы так часто встречаются в природе — случайность или фундаментальный принцип устройства мира?