Как я измерял ускорение свободного падения
Автор: Влад НордвингCразу после Нового года я ударился в идиотию заклёпочничество. Зачем мне это надо? Затем, что Главной Героине моей книжки пришла фантазия измерить ускорение свободного падения с помощью маятника. Классический школьный опыт.
Мои юные герои вместе с родителями живут в некоем странноватом доме, у которого минимум 10 или 15 этажей, а может и больше (сколько на самом деле, они не знают). Некоторые этажи очень высокие (20 или даже 30 метров), а другие обычной высоты. И вот моей Главной Героине в силу шилозадости захотелось применить физику на практике. Известно, что величина ускорения свободного падения уменьшается с высотой, и этот градиент известен. Значит (рассуждает моя Героиня), измерив УСП в подвале дома и на чердаке дома, можно узнать разницу, и стало быть, грубо оценить его высоту. (Метод подобных треугольников, как в «Таинственном острове» Жюля Верна, по сюжетным ограничениями применить нельзя.)
Я решил, что неплохо бы сначала проделать такой опыт самому, как поступали все добросовестные естествоиспытатели. Главная моя задача такая: нужно было понять, достаточна ли точность этого метода, могут ли подростки получить значимый результат, превышающий статистическую погрешность? (Спойлер: в итоге точность метода оказалась недостаточна даже для детей, живущих в далёком будущем. Уже переделываю сюжет.)
Здесь под катом все формулы, если кто-то интересуется:
Итак, наука установила, что период колебаний математического маятника подчиняется формуле:
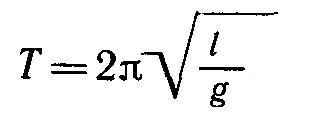
где T — тот самый период колебаний, l — длина подвеса, то есть верёвки, на которой висит наша гиря, а g — это и есть УСП.
Это легко преобразовать и вывести уравнение для g:
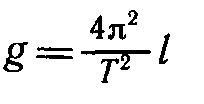
Легко видеть, что определить УСП весьма просто — нужно сначала измерить длину верёвки, а потом заставить маятник качаться и посчитать период его колебаний. Подставить две переменных в формулу, и найти искомое. При этом масса гири не важна, её в формуле нет.
Как найти период колебаний?
Это понимает каждый, кто учился в школе и не прогуливал физику. В советской школе, по крайней мере, за «поколение ЕГЭ» я ручаться не могу. Итак, период колебаний это время, которое проходит между двумя одинаковыми положениями маятника (если что, это я рассказываю своими словами, а не «по учебнику»). Вот перед нами качается маятник, мы запускаем часы в момент, когда он находится в крайнем левом положении, и выключаем когда он в это же положение возвращается после одного полного качания.
Но если у нас нет суперточных часов, то одно измерение даст слишком сильную погрешность. Надо позволить маятнику сделать несколько качаний, засечь общее время, и взять среднее. Имеем:
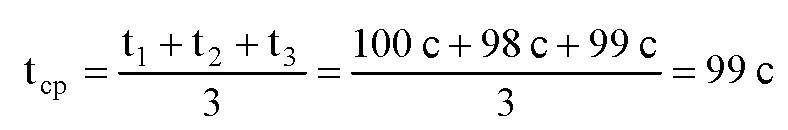
Это формула и пример решения, как мы вычисляем среднее время качаний маятника. Здесь t1, t2 и t3 — это время, за которое маятник сделал, например, сорок полных качаний. В этой конкретной формуле мы пронаблюдали три таких серии по 40 колебаний, поэтому и делим сумму t1+t2+t3 на три. Для увеличения точности можно провести не три, а 10 или 100 таких серий.
После этого вычисляем средний период колебаний:
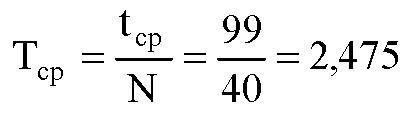
Здесь полученное значение среднего времени мы делим на количество колебаний в каждой серии, то есть на сорок. И опять же, для увеличения точности можно дать маятнику качаться не 40, а 80 раз, или больше. Насколько хватит терпения сидеть и пялиться на него. Хотя, чем их больше, тем больше и вероятность сбиться со счёта во время эксперимента.
Вот мы получили средний период колебаний нашего маятника, и теперь можем вычислить среднее значение УСП:
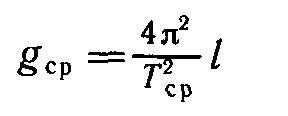
Конечно же, это наше значение будет отличаться от истинного. Потому что:
- наш маятник не математический, а очень даже физический; его нить способна растягиваться под весом груза (то есть менять длину), что вносит искажения;
- масса груза и масса нити вполне себе сопоставимы; то есть нить сама по себе может рассматриваться как бесконечное число маленьких маятников с разной длиной;
- маятник качается не в вакууме, а в воздухе, что его тормозит;
- на маятник действует куча всяких мелких факторов, от колебаний пола комнаты из-за проезжающей по дороге машины, до моего сердцебиения;
- и так далее.
Всё это вместе ведёт к тому, что измеренное значение УСП будет отличаться от истинного на данной высоте над морем. И нужно найти относительную погрешность наших измерений:
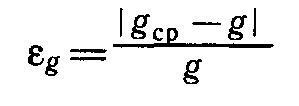
Почему погрешность относительная? Вот потому, что измеренные значения мы сравниваем с истинным значением – «относительно» него, то есть. И эта погрешность есть разность нашего вычисленного значения и истинного значения УСП, которое мы берём по модулю и делим на истинное значение. То есть как в формуле.
Можно посчитать и абсолютную погрешность измерений, но она нам в данном случае не очень-то и нужна.
Большинство из перечисленных выше факторов погрешностей мы устранить не сможем. Но мы можем минимизировать самый значительный из них, а именно первый — приблизить наш маятник к математическому. Для этого нужно:
- Снизить массу нити и увеличить массу груза. До тех пор, пока нить его ещё держит и не рвётся.
- Отклонять маятник всего на несколько сантиметров, чтобы он качался чуть-чуть. Этим сводятся к минимуму искажения от растяжения нити, да и от сопротивления воздуха тоже.
Кроме всего вышенаписанного, есть способ ещё увеличить точность измерений. Это формула Бесселя. Он предложил брать для вычислений два периода колебаний, при двух разных длинах нити. Сам маятник при этом должен оставаться тот же. Получается вот такая формула:
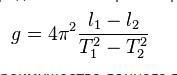
Видно, что это то же самое, что и формула (5), только фигурируют не абсолютные значения, а разницы T и l.
Я взял пластиковую верёвку, моток которой нашёлся в шкафу. В качестве груза у меня была маленькая пластиковая бутылка из-под воды. Я натолкал туда гаек и старых батареек.
На следующем шаге пришлось освоить два морских узла, схемы которых нашёл в Сети. Беседочный узел, чтобы привязать верёвку к люстре, и эшафотный, чтобы сделать утолщение на другом конце – дырка в крышке бутылки оказалась великовата, и обычные узелки сквозь неё проскальзывали.
Взял мобильник, нашёл в нём секундомер. Отклонил бутылку всего сантиметров на пять и отпустил. В момент одного из экстремумов запустил секундомер. Через 40 полных качаний выключил. Записал, сколько прошло секунд. Повторил всё это 18 раз.
Быстро выяснилось, что моя коша очень заинтересовалась этой движухой. Пришлось попросить её немного погулять в коридоре, иначе эксперимент мог закончиться падением люстры.
После первой серии я укоротил верёвку и повторил всё снова. Период колебаний немного уменьшился, что естественно.
Потом я снял всю конструкцию с люстры, пригласил в комнату кошу и начал обрабатывать результаты. Все значения оказались сведены в таблице:

Первым делом я отбросил самые меньшие и самые большие значения. Получилось 16 измерений для каждой длины подвеса. И осталось просто подставлять цифры в формулы. Получилось:
Длина 2,33 м — УСП 9,5961 м/с^2
Длина 2,17 м — УСП 9,5759 м/с^2
Результаты, прямо скажем, не блестящие. Однако, они очень близкие, а значит, опыт проведён верно. Отклонение от истинного значения, которое на поверхности Земли равно в среднем 9,81 м/с^2 вызвано, конечно, кустарностью моей конструкции.
Эти формулы описывают математический маятник, а не физический. Моя верёвка не сильно, но всё же растягивается под грузом. Груз качается в воздухе, что его тормозит. В идеале, подвес должен быть очень жёсткий, не тянуться совсем, и очень лёгкий,чтобы не вносить искажений в измерения. А груз должен быть не бутылочка с гайками, а, например, маленькая гирька в 10 килограмм. Из чугуна. Или лучше из урана. И всё это нужно поместить в вакуум. И на амортизаторы. Тогда, может быть, получились бы близкие в истине значения.
Кроме того, я обнаружил, что в ходе процесса начинаются эволюции, похожие на движения маятника Фуко. Сначала груз качается как положено, а потом плоскость превращается в эллипс. И более того, большая ось этого эллипса начинает весьма заметно поворачиваться. То есть – при начале отсчёта времени бутылка качалась прямо вдоль ковра, а при остановке секундомера она уже описывает почти круг, причём поперёк ковра. Порядочные математические маятники так себя не ведут.
Напоследок я высчитал УСП по формуле Бесселя. Для этого я и провёл изначально два измерения с разной длиной подвеса. Формула есть под катом выше.
У меня получилось УСП — 9,8781 м/с^2
Это уже ближе к истине. Бессель как раз и предложил эту формулу, чтобы повысить точность измерений. В ней операции проводятся не над абсолютными значениями, а над разностями длин подвесов и периодов колебаний.
Какие же выводы?
Казалось бы, всё более-менее неплохо? На самом деле нет. Среднее УСП на уровне моря на планете Земля составляет 9,8066 м/с^2. А на уровне 1 километр над морем оно составляет 9,8036 м/с^2. Разница в третьем знаке после запятой, а у меня только во втором. Ошибка больше чем на порядок! Причём, при разнице высот целый километр! Дом моих героев явно поменьше. Одним словом, это неприемлемая погрешность.
Проще говоря, этот способ недостаточно точен для того, чтобы можно было его применить для измерения высоты строений, даже очень грубого. Моим героям пришлось бы на два порядка (в сто раз) повысить его точность. Увы, для школьников, пусть и в далёком будущем, это не под силу.
Конечно, я немного порассуждал о том, нельзя ли тут применить «метод фантдопов». То есть, предоставить в их распоряжение отлично оборудованную лабораторию, где можно было бы найти всё необходимое оборудование:
- очень тонкая и почти невесомая нить из углеродных нанотрубок;
- какой-нибудь лазерный измеритель длины подвеса маятника с точностью до нанометров;
- сверхточный таймер, измеряющий период качаний с точностью до третьего знака;
- герметичный прозрачный ящик на амортизаторах;
- вакуумный насос нужной производительности, вместе с компактным источником питания для него.
Дальше можно не продолжать. Получится научная статья, а не фантастический роман. Тупо скучно.
Вывод: придётся переделывать план книги. Вернее, той части, которая относится к исследованию моими героями странностей своего мира. Придумывать для них какой-то другой способ применить свои школьные знания.
