Межпланетные транспортные системы. Часть 2. Электрические межпланетные корабли

В предыдущей части мы видели что обычных химических ракетных двигателей вполне достаточно для полета к ближайшим небесным телам солнечной системы при условии что топливо на обратный путь добудем на месте. Однако если мы хотим лететь быстрее, либо туда, куда дельты "Старшипа" уже не хватает то придется либо брать с собой много танкеров, возможно расходуемых, либо искать двигатель с большей скоростью истечения. Такой двигатель существует и используется в современной космонавтике. Это электроракетные двигатели, делящиеся по принципу создания тяги на ионные (разгон холодной плазмы электростатическим полем) и плазменные (разгон горячей плазмы магнитным полем).

Общеизвестно то что тяга ионных двигателей мала. Но судя по регулярным репликам в интернетах "ну это пока маленькая - сейчас разработают с большой" не все понимают почему она мала. Дело в том что мощность, требуемая для питания электроракетного двигателя (P, Вт), выражается формулой:

P*КПД = F*W/2

где F - тяга (Н), W - скорость истечения топлива (м/с), КПД - КПД в относительных единицах. Скорость истечения нам нужна по-больше для формулы Циолковского. Допустим для простоты 10 000 м/с. Тогда для тяги 1 Н при КПД = 1 (т.е. 100 %) получим потребляемую мощность в 5 кВт. На всего один Ньютон. Ради тяги в одну тонну или 10 кН потребуется 50 МВт и это без учета КПД. Вот только электростанцию скорее всего придется везти с собой (передача лазером с некоей внешней станции уже практически внешне приводу который отдельная тема). А электростанция на 50 мегаватт весит совсем не тонну. То есть на самом деле не тяга двигателей мала, а электростанция тяжелая. Сами двигатели пока что в пересчете на Ньютон тяги тоже не легкие, но на данный момент ускорение ионолета лимитирует именно источник энергии.

Скорость истечения в 10 км/с еще не сильно лучше химических двигателей. Сейчас для довыведения спутников на геостационар используются двигатели со скоростью истечения 16-30 км/с. Резон повышать скорость у ионных двигателей еще и в том что затраты энергии на ионизацию рабочего тела постоянны и с ростом скорости истечения их вклад в КПД падает. Энергия отрыва первого электрона практически всех (может и всех - лень всю таблицу проверять) химических элементов чуть более 1 МДж/моль вещества в атомарном состоянии. Т.е. для водорода будет жуткий гигаджоуль на килограмм. При скорости истечения 10 км/с кинетическая энергия килограмма водорода будет только 50 МДж, т.е. даже если процесс собственно разгона имеет КПД 100 % - суммарный КПД такого ЭРД будет никакой из-за потерь на ионизацию водорода. В случае с горячей плазмой полной ионизации в теории не обязательно - главное чтобы по плазме ток шел. Но в ионных уже так не получится. С другой стороны, если разгонять водород до 100 км/с - кинетическая энергия килограмма рабочего тела будет уже 5 ГДж - в пять раз больше чем потрачено на полную ионизацию.

На практике ионных и плазменных двигателей на водороде не делают. Делают на ксеноне и криптоне имеющих атомную массу 131 и 84, что снижает потери на ионизацию пропорционально атомной массе. Другая причина использовать инертные газы - при использовании химически-активных веществ будет разрушение конструкции свободными радикалами в зоне контакта с плазмой. Проблема в том что благородные газы в Системе можно намайнить очень не везде. Но есть и всеядный электроракетный двигатель - пульсирующий индукционный. Это разновидность плазменного двигателя в котором генерация плазмы производится безконтактно переменным магнитным полем.

У кислорода энергия ионизации килограмма в 16 раз ниже чем у водорода. При скорости истечения 50 км/с кинетическая энергия килограмма рабочего тела грубо гигаджоуль. Итого для воды или СО2 в пульсирующем двигателе достижимы "50 на 50" - КПД 50 % на 50 км/с скорости истечения. Скорее всего КПД будет даже выше, но возьмем с запасом. На ньютон тяги при таких параметрах нам требуется 50 кВт электричества. Теперь  можно перейти к ускорениям со скоростями.

На данный момент используются солнечные батареи.

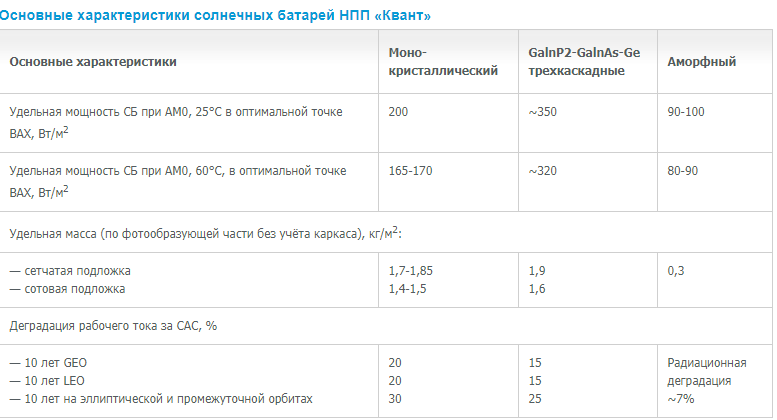
Массу в месте с каркасом возьмем равной 3 кг/м2. Согласно таблице, с этого квадратного метра можно получить 350 Вт. Итого ~120 Вт/кг. Округлим до 100 Вт/кг и получим 500 кг батарей для нашего искомого Ньютона тяги. Если на сами ПИДы, рабочее тело и полезную нагрузку у нас еще пол тонны массы - будем иметь ускорение 0.001 м/с2. Кажется что за 3 400 000 секунд при старте с НОО вы наберете заветную вторую космическую? Так вот, не наберете. Чтобы убедиться в этом нам понадобится нижеследующий скрипт на Python (вместо отступов нижние подчеркивания):

import math

G = 6.674*(10**-11)

M = 5.97*(10**24)

GM = G*MX = [6578000,0]

V = [0,7800]

at = 0.001

T = 3400000

for t in range(T):

____r = math.sqrt(X[0] * X[0] + X[1] * X[1])

____a = [-X[0] * GM / (r * r * r),-X[1] * GM / (r * r * r)]

____V = [V[0] + a[0],V[1] + a[1]]

____v = math.sqrt(V[0] * V[0] + V[1] * V[1])

____V = [V[0] + at * V[0] / v, V[1] + at * V[1] / v]

____X = [X[0] + V[0], X[1] + V[1]]

v2 = math.sqrt(math.sqrt(a[0] * a[0] + a[1] * a[1]) * r)*math.sqrt(2)

print(math.sqrt(V[0] * V[0] + V[1] *V [1]))

print(v2)print(r/1000)

Данный скрипт рассчитывает движение спутника произвольной массы по орбите вокруг Земли с постоянным ускорением at направленным строго по направлению движения за время T. Все размерности в СИ. Спутник стартует с околоземной почти-круговой орбиты (высота 200 км, скорость 7800 м/с). Скрипт выводит в консоль три значения: модуль скорости, вторую космическую для данной высоты и радиус орбиты в километрах в конце симуляции. За те самые 3 400 000 секунд у нас получается следующее:

4371.5116572435

6177.989868719956

20878.348646810908

Опа, мы так и не набрали вторую космическую! А все дело в том что пока мы медленно и печально разгонялись — гравитация нас столь же медленно тормозила. А при быстром ускорении на ЖРД у земного притяжения было бы на порядки меньше времени для своей подрывной деятельности — для них дельты не на много больше теоретических в чем можно убедиться хоть в KSP (с модом RSS), хоть из реальной грузоподъемностей ракет на отлетную траекторию. Набрать вторую космическую с ускорением в 0.001 м/с получится только за ~7.2 миллиона секунд. Что означает дельту-вэ в 7.2 км/с вместо теоретических 3.4 км/с и практических 3.8 для презренной химии.

Эффект Оберта

Частный случай гравитационных потерь. Просто набрав вторую космическую мы сможем либо слетать к Луне, либо выйти на гелиоцентрическую орбиту близкую к земной. Чтобы полететь, например, к Марсу нам нужно прибавить еще скорости к орбитальному движению Земли. Порядка 3 км/с. Вот только ракета с ЖРД или твердофазным ЯРД разогнавшись в глубине гравиямы до скорости чуть выше второй космической на выходе из сферы Хилла будет иметь совсем не разность своей скорости со второй космической. Дело в том что для выхода из потенциальной ямы нужна не скорость, а энергия. Которая просто соответствует некоторой скорости. И квадрат скорости по выходу из сферы Хилла будет равен разности квадратов скорости на старте и второй космической. В результате для отлета к Марсу с НОО кораблю с ЖРД требуется около 4 км/с. А вот с ЭРД — все 10 км/с.

И что делать?

Можно прокачать ЭРД настолько чтобы гравипотери были не существенны на фоне располагаемой им дельты. Но при ускорении 0.001 м/с2 до 30 км/с разгоняться год. При этом запас рабочего тела при скорости истечения 50 км/с уже будет около трети стартовой массы, а нам надо куда-то воткнуть ПН, двигатели и прочие солнечные батареи. Короче говоря, надо повышать удельную мощность. А можно использовать ЭРД для перелетов вне гравитационных колодцев планет. В межпланетном пространстве ЭРД позволяет либо уменьшить время перелета разогнанного на химии корабля, либо перетаскивать хорошо защищенный от радиации «хайлайнер» между орбитами с минимальным расходом рабочего тела. Еще один питоновский скрипт:

import math

G = 6.674*(10**-11)

M = 1.98*10**30

GM = G*MX = [150*10**9,0]

V = [0,33000]at = 0.0001

dt = 24*3600

T = 365

for t in range(T):

____r = math.sqrt(X[0] * X[0] + X[1] * X[1])

____a = [-X[0] * GM / (r * r * r),-X[1] * GM / (r * r * r)]

____V = [V[0] + a[0] * dt,V[1] + a[1] * dt]

____v = math.sqrt(V[0] * V[0] + V[1] * V[1])

____V = [V[0] + at * V[0] * dt / v, V[1] + at * V[1] * dt / v]

____X = [X[0] + V[0] * dt, X[1] + V[1] * dt]

____if t % 10 == 0:

________print(t)

________print(r/(1000*1000*1000))

________print('------')

Моделирует разгон доразгон электролёта со скоростью относительно Солнца 33 км/с с ускорением 0.0001 м/с2. И печатает количество дней после старта и радиус орбиты (в миллионах километров) каждые 10 дней. За 200 суток полета корабль достигнет высоты орбиты Марса в афелии — 250 миллионов км. Перигелий Марса будет достигнут между 120 и 130 сутками полета. Если же убрать дополнительное ускорение занулив at — апогей орбиты в 242 миллиона км будет достигнут лишь на 260 сутки. Т.е. мало того что лететь заметно дольше, так еще и есть возможность недолета в неудачный год. Очевидно что чем дальше наша цель — тем эффективней доразгон.

В расчете взято ускорение 0.0001 м/с2 что означает что на солнечные батареи уйдет только 5 % массы, а не 50 % как в случае 0.001 м/с2. Тому самому Старшипу нужно 10 тонн солнечных батарей. Для Марса в этом нет особого смысла - того же эффекта можно достичь просто подогнав 5 танкеров вместо 4. А что если лететь дальше? Немного усложним наш скрипт для учета зависимости мощности (и тяги) от расстояния до Солнца и увеличим время интегрирования до 400 суток.

import math
G = 6.674*(10**-11)
M = 1.98*10**30
GM = G*M
X = [150*10**9,0]
V = [0,33000]
dt = 24*3600
T = 400
for t in range(T):
____at = 0.0001
____r = math.sqrt(X[0] * X[0] + X[1] * X[1])
____at = at * (150*10**9) * (150*10**9) / (r * r)
____a = [-X[0] * GM / (r * r * r),-X[1] * GM / (r * r * r)]
____V = [V[0] + a[0] * dt,V[1] + a[1] * dt]
____v = math.sqrt(V[0] * V[0] + V[1] * V[1])
____V = [V[0] + at * V[0] * dt / v, V[1] + at * V[1] * dt / v]
____X = [X[0] + V[0] * dt, X[1] + V[1] * dt]
____if t % 10 == 0:
________print(t)
________print(r/(1000*1000*1000))
________print('------')

Увидим что к афелию Марса электролет придет не сильно после разгонявшегося равномерно - между 200 и 210 сутками. Но после 350 суток полета расстояние до Солнца начнет уменьшаться - корабль перейдет на нисходящую половину эллипса орбиты. Из общефизических соображений следует что двигатель малой тяги будет эффективней на орбите близкой к круговой, а на солнечной электростанции - вблизи Солнца. Поэтому лучше стартовать с земной орбиты (V=[0, 29780]) и имея ускорение по-больше. Повысив at до 0.0005 получим достижение афелия Марса между 210 и 220 сутками полета. За 400 суток полета корабль гарантированно достигнет Цереры.

Теперь у нас только на батареи 25 % массы. Поставить на "Старшип" малой кровью уже не получится. Нужно мыслить стратежней и строить то что я решил назвать хайлайнером в честь кораблей из "Дюны": корабль который будучи один раз выпнут из гравиямы планеты туда больше не заходит. А принимает те же "Старшипы", которым достаточно набрать лишь вторую космическую местной планеты. хайлайнер летит долго но может иметь все необходимое для комфортного проживания: центрифугу, ЗЭ СЖО, радиационную защиту, блэкджек и шлюх.

За год под ускорением 0.0005 м/с2 хайлайнер потратит 15 км/с дельты. При скорости истечения 50 км/с рабочего тела нужно 26 % стартовой массы. Одним словом надо повышать удельную мощность. Для солнечно-электрического хайлайнера самый простой способ - подлететь ближе к Солнцу. Развернем вектор тяги на 180 (at = -0.0005). за 200 суток наш хайлайнер подойдет к Солнцу на 50 миллионов км и увеличит мощность батарей в 9 раз. Проблема лишь в том что начав разгоняться вблизи звезды мы быстро уйдем от нее. Однако если нам нужно поменять наклонение орбиты причем вблизи светила - солнечные батареи весьма неплохой вариант.

Удельную мощность солнечных батарей можно нарастить повысив КПД - экспериментально подтверждена возможность 50 %, что дает 600 Вт/м2 на орбите Земли или уменьшив вес конструкции. Проблема в том что взятые для расчета 3 кг/м2 соответствуют миллиметровым толщинам кремния и полимерной подложки. Со всеми ухищрениями можно ожидать увеличения удельной мощности еще на порядок, но не более. Может попробовать ядро?

Человек звучит гордо. Обезьяна - перспективно

Это про солнечные и ядерные космические электростанции. В близи Земли ядерные источники энергии пока что проигрывают солнечным батареям по удельной мощности катастрофически. Топаз-40/100, самый мощный из условно-существовавших имел 22 кВт/т - в 5-6 раз хуже солнечных батарей.

Как увеличить удельную мощность космического ядерного реактора? Ожидаемый ответ при виде характеристик "А повысьте КПД" не верен. КПД в первом приближении определяется разницей температуры реактора и "холодильника" тепловой машины производящей энергию. Наращивать температуру реактора - плохая идея. Уменьшать температуру холодильника - тоже ибо интенсивность излучения с холодильника зависит от температуры в четвертой степени.

Допустим температура радиатора 1000 К. По закону Стефана-Больцмана с квадратного метра радиатора будет излучаться до 57 кВт. А если у радиатора две стороны - все 114 кВт. У нас есть энергоустановка мощностью пусть 100 МВт и с КПД 10 % при температуре холодного конца 1000 К - нам надо излучить 900 МВт. Для этого нам надо 9000 м2 радиатора. Но мы решили что расточительно так расходовать энергию и поставили вместо радиатора еще одну тепловую машину. С горячим концом 1000 К и холодным ну пусть 500 К. Из-за четвертой степени в законе Стефана-Больцмана наши радиаторы теперь излучают в 16 раз хуже. Но даже цикл Карно при такой разности температур будет иметь КПД 50 %. Хотите холодный конец в 100 К? да пожалуйста но по идеальному циклу Карно это КПД 90 %, а вот излучающая способность радиаторов ухудшится в 10000 раз. Если вместо каскада тепловых машин ставить одну тепловую машину будет то же самое. Но каскад реалистичней ибо сложно организовать работу одной ТМ при столь большой разнице температур.

В пределе больших мощностей масса ЯЭУ определяется массой радиаторов. А повывшая КПД через уменьшение температуры радиаторов мы эти радиаторы утяжеляем. Близкой к оптимальной видится температура 1000 К - та же сталь еще не плавится и при этом хорошая излучающая способность. Даже при КПД 10 % квадратному метру радиаторов будет соответствовать 10 кВт полезной мощности которые будут независимо от расстояния до звезды. Правда квадратный метр радиаторов скорее всего будет весить больше чем квадратный метр солнечных батарей. Но даже если делать из стального листа толщиной 0.5 мм масса будет лишь 8 кг/м2 при том что стальной радиатор может быть самонесущим. Ура, теоретическое ограничение мощности уже порядка 1 кВт/кг.

Теперь мы можем взять скорость истечения 100 км/с, на всякий случай оставить КПД 50 %. 100 кВт на Ньютон, энергоустановка весит 100 кг - в 5 раз меньше солнечной. Обновленный ядерно-электрический хайлайнер с ускорением 0.001 м/с2 может за год достичь Юпитера. Проблема лишь в том что от еще бумажного проекта "Нуклон" до гипотетической ядерной энергетической установки с удельной мощностью 1 кВт/кг путь как от самолета братьев Райт до магистрального авиалайнера.