Космический бой и принцип относительности наглядно

В коде была ошибка. Исправил и пересчитал графики. Спасибо Наблюдателю за наблюдательность.

По результатам сра дискуссии в одном чате чтоб добро не пропадало.

Есть мнение что космические бои вроде такого

Невозможны. Потому что «скорости в десятки километров в секунду». И что «огромные ускорения понадобятся чтоб маневрировать». Люди, скорость всегда относительно чего-то. В данном конкретном случае — относительно убегающего корабля. И догоняющие могут выбрать себе такую скорость чтобы атаковать было удобней. Короче, написал я срипт на языке Scilab (мне в нем проще графики рисовать):

clear//очищаем память на всякий случай

V0 = [20;0]// начальная скорость синего корабля, вектор, километры в секунду

V1 = [21;0]// начальная скорость красного корабля, вектор, километры в секунду

x0 = [50;0]// начальные координаты синего корабля, километры

x1 = [0;10]// начальные координаты красного корабля

dt = 0.01// шаг симуляции

a0 = 0.005// ускорение синего, километры в секунду за секунду

a1 = 0.01// ускорение красного, километры в секунду за секунду

N = 600/dt// количество шагов симуляции

X0 = zeros(2,N)//массив координат синего

X1 = zeros(2,N)//массив координат красного

X = zeros(2,N)//массив координат красного относительно синего

R = zeros(1,N)//массив расстояний от красного до синего

V = zeros(1,N)//массив модулей скорости сближения от красного и синего

for i = 1:N //мотаем цикл

X0(:,i) = x0//записываем координаты

X1(:,i) = x1//записываем координаты

x = x1-x0

X(:,i) = x//записываем координаты

R(i) = sqrt(x(1)*x(1)+x(2)*x(2))//считаем расстояния

v = V1-V0

V(i) = sqrt(v(1)*v(1)+v(2)*v(2))//считаем скорости

x0 = x0+V0*dt//перемещаемся с текущей скоростью

x1 = x1+V1*dt//перемещаемся с текущей скоростью

V0 = V0+a0*dt*(x0-x1)/R(i)//убегаем

V1 = V1+a1*dt*(x0-x1)/R(i)//догоняем

end

figure(1)//создаем графическое окно

plot(X0(1,:),X0(2,:),'.b',X1(1,:),X1(2,:),'.r')//рисуем график

xlabel('X, km')

ylabel('Y, km')

figure(2)//создаем графическое окно

plot(0,0,'.b',X(1,:),X(2,:),'.r')//рисуем график

xlabel('X, km')

ylabel('Y, km')

figure(3)//создаем графическое окно

plot([1:N].*dt,R(:),'r')//рисуем график

xlabel('Time, s')

ylabel('R, km')

figure(4)//создаем графическое окно

plot([1:N].*dt,V(:),'r')//рисуем график

xlabel('Time, s')

ylabel('V, km/s')

скрипт моделирует два корабля имеющие начальные скорости 20 (синий) и 21 (красный) км/с относительно чего-то. Назовем это чего-то Инерциальной Системой Отсчета или просто Системой. Красный пытается догнать синий ускоряясь тупо в его сторону с ускорением 10 м/с2, синий точно так же тупо убегает ускорением 5 м/с2. По умолчанию время симуляции 600 секунд, шаг 0.01 секунды.

Скрипт выводит четыре графика:

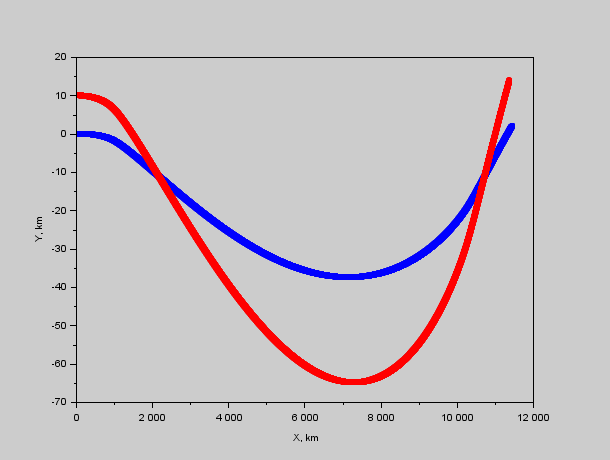
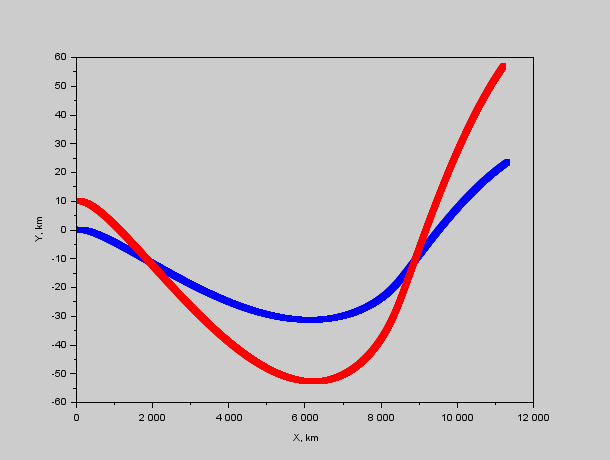
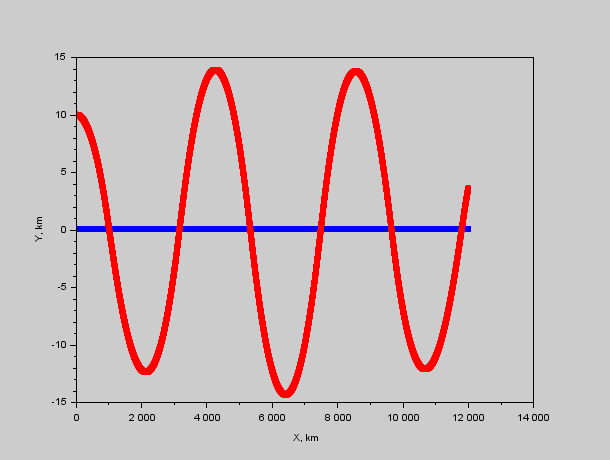
Рис. 1. Траектории кораблей относительно Системы. Видно что красный быстро пролетает мимо синего, после чего разворачивается и цикл повторяется.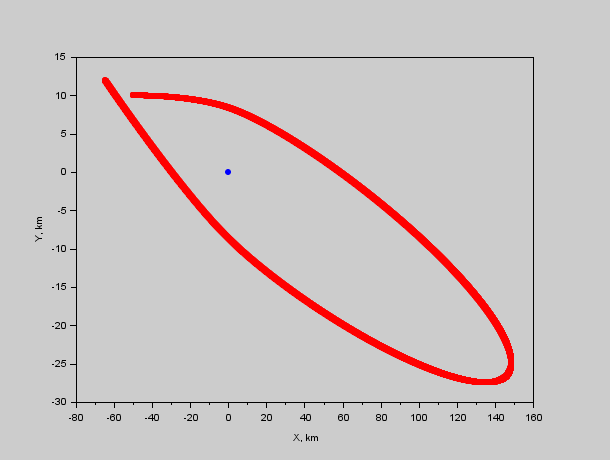

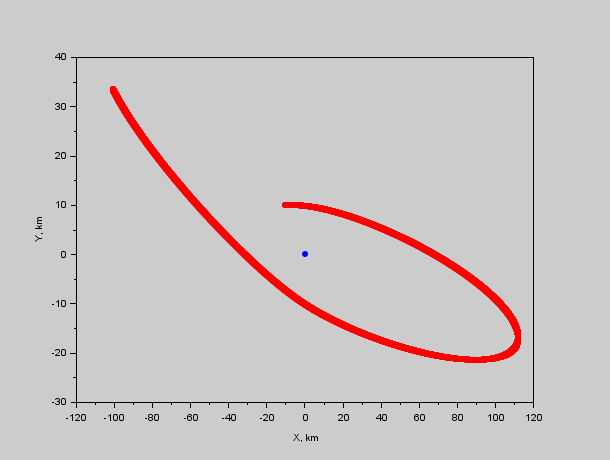
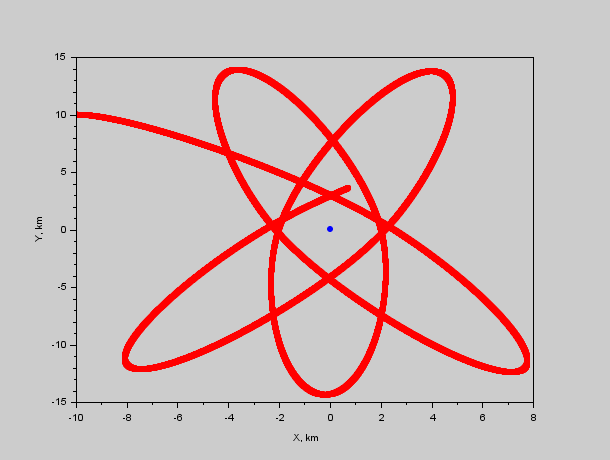
Рис. 2. Траектория красного относительно синего. Видно что преследователь будет крутиться вокруг жертвы сближаясь и отдаляясь.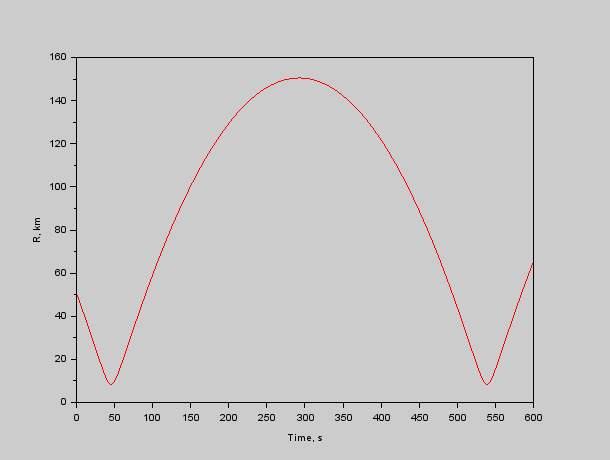

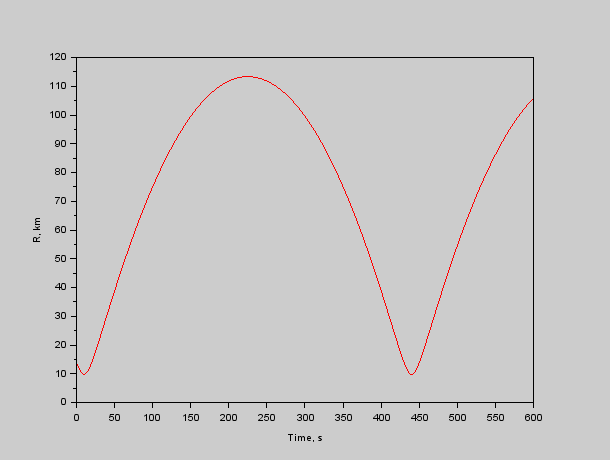
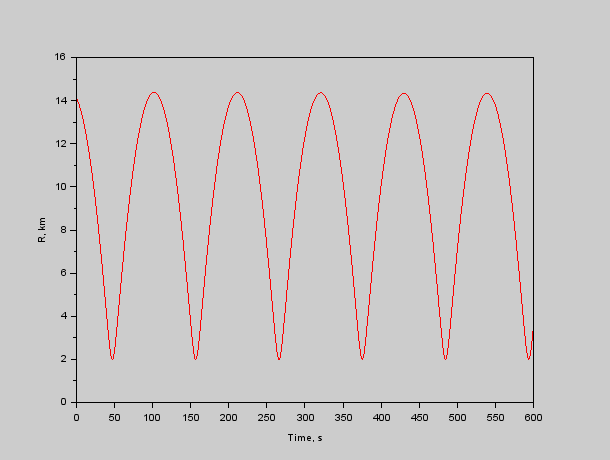
Рис. 3. Расстояние от красного до синего.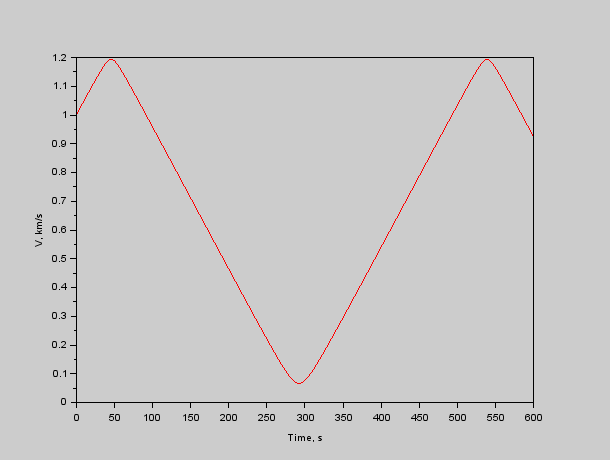

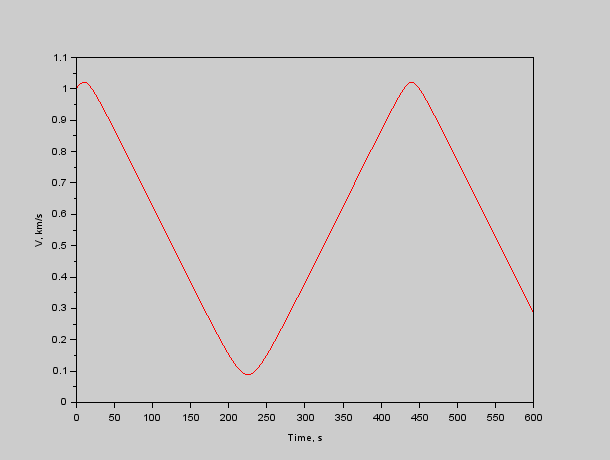
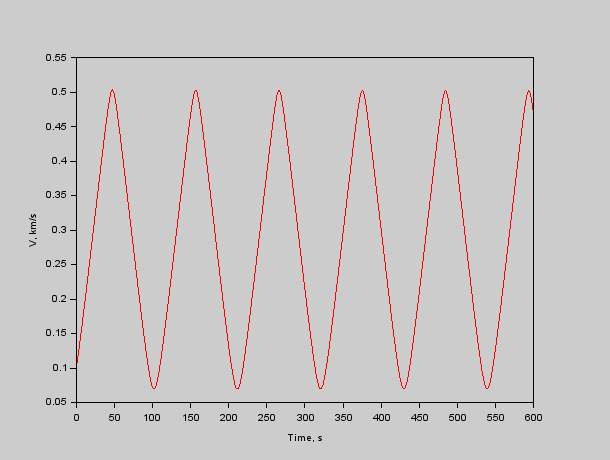
Рис. 4. Модуль скорости красного относительно синего.

Как видно из графиков, корабли периодически сближаются до 10 км. При этом максимальное сближение соответствует максимальной же относительной скорости. Т.е. красный корабль будет периодически делать «вжух» возле синего на скорости 1.2 км/с. Что уже вполне «земная» скорость, хотя ближе к реактивной авиации, чем к поршневой.

Я в курсе о существовании пропорционального наведения, но тут красному надо сблизиться с синим чтобы пострелять и после улететь из зоны ответного огня, а не протаранить.

Поменяв в коде начальные координаты

x0 = [10;0]// начальные координаты синего корабля, километры

x1 = [0;10]// начальные координаты красного корабля

получим следующие графики:

Дистанция вжуха и его скорость почти не изменились. Потому что красный корабль изначально догонял синий с превышением скорости 1 км/с. Но кто ему мешает сбросить скорость? Допустим до 20.1 км/с (V1 = [20.1;0])

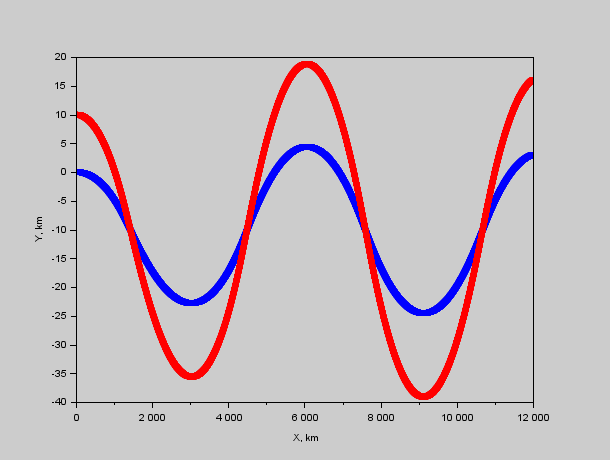
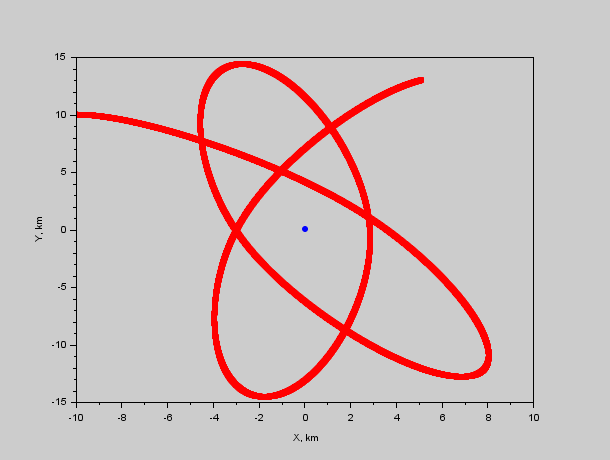
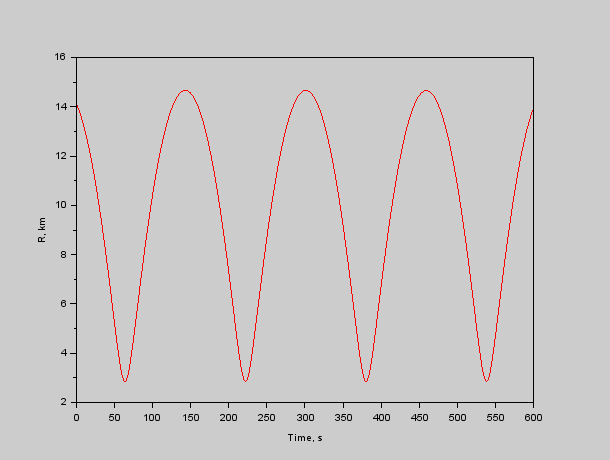
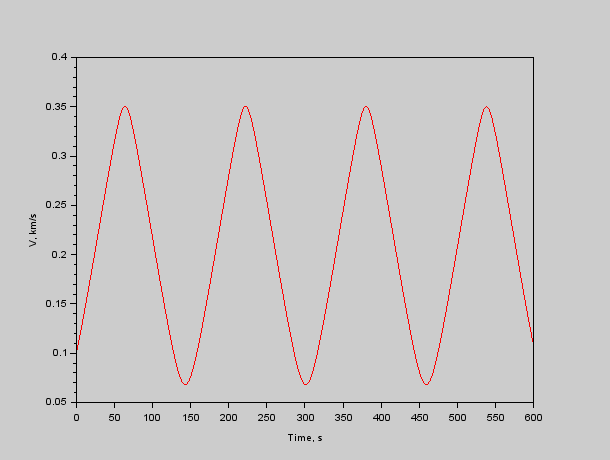
И теперь мы видим хоть и не ВМВ, но точно Корею или Вьетнам в космосе. Скорость при максимальном сближении 350 м/с — чуть выше звуковой, сближение до 3 километров.

Теперь допустим что синий решил не убегать в виду бесполезности этого занятия (a0 = 0):

Видим что убегать было и правда малополезным занятием ибо особой разницы по скорости и дистанции это не дало, при том что маневрирование требует тратить топливо и мешает использовать надувные ложные цели.

Вывод. Догоняющий корабль имея преимущество в ускорении может выбирать скорость и расстояние максимального сближения вплоть до буквально «как во Вторую Мировую». Зачем ему это? Например затем что раз уж он погнался за синим кораблем то наверно хочет в него пострелять, а стрелять подлетев ближе и имея больше времени на прицел удобней.