О вероятностях, выборках и данном по факту

Возрождение дискуссии о тухлых пирожках заставило сформулировать одну мысль. 

Когда люди считают вероятность какого-то события, в рамках решения задачи или просто прикидывая по жизни, они часто не понимают, из каких вариантов вообще ведется выбор. И равновероятны ли они. Видимо, потому, что у них плохо развито умение представить себе ситуацию. Поэтому они подменяют одни условия другими и решают совсем не ту задачу, которую им предложили решить.

Если с тупым упрямством считать разновероятные события как равновероятные, решение не выдержит проверки простым суммированием (вероятности всех событий из выборки возможных должны равняться 1) или проверкой всей выборки (в случае с пирожками - вскрываем все контейнеры и смотрим, сколько из них соответствуют условию). 

Допустим, у нас возможны 4 события. Например, у нас есть 2 ящика, в каждом лежит два шарика, вероятность достать какой-то из них из любого ящика - 1/4 (1/2, что шарик в этом ящике, * 1/2, что мы достанем его, а не второй). А теперь представим, что какой-то один шарик мы уже достали. Если мы не положим его обратно, мы уже не можем достать его же вторым, третьим или четвертым. Если положим, то можем - с той же вероятностью 1/4. Но, поскольку ящиков у нас 2 и шарики лежат попарно, то, вводя условие "берем второй шарик из того же ящика", мы отсекаем автоматически 2 шарика, лежащих в другом ящике. Если бы ящик был один, то они остались бы нам доступны. Но если по условию задачи первое, что мы делаем, это выбираем наугад ящик, то мы автоматически себя ограничиваем и выбираем дальше из того, что лежит в ящике. 

Или, например, возьмем монетки. Вероятность выбросить одновременно две решки - 1/4. Вероятность выбросить решку - 1/2. И если у вас одна монета уже решкой кверху лежит и это дано, то реализуется именно вероятность 1/2. Вероятность выбросить два орла, таким образом, равна 0, и вероятность выбросить орла и решку равна 0, вы можете получить либо решку и орла, либо две решки. 1/2+1/2=1

Поэтому очень важно понимать, где и в какой момент условие задачи отсекает определенные вероятности, делая их равными 0. 

На житейском примере: если вы решали, позвать с собой на пьянку Дашу или Машу (обе в 50% случаев напиваются до положения риз и готовы на все, в половине случаев ведут себя прилично, живут в разных местах), и позвали Дашу, а Маша с вами пить не пошла, то вы уже вряд ли окажетесь в постели с пьяной Машей. С Дашей - можете. У нас 50% вероятность, что она напьется и вам даст. 

Вернемся к нашим ящикам. Допустим, что в них 3 белых и 1 черный шар. Опять выбираем наугад ящик, достаем оттуда шар и смотрим на него. Если мы достаем черный шар, то реализуется единственная возможная комбинация ЧБ с вероятностью 1/4. Но поскольку она уже по условию реализовалась, то ее вероятность не имеет значения. Второй шар в том же ящике может быть только белым, не потому что все остальные шары белые, а потому, что в ящике с черным шаром вторым лежит белый шар. 

Если мы достаем белый шар, то у нас реализовалась вероятность 3/4. Комбинации Б1Б2, Б2Б1 и БЧ. Но она опять-таки по условию реализовалась, когда ящик мы уже выбрали. Поэтому, если мы выбрали ящик ББ и получили возможные комбинации Б1Б2+Б2Б1, то, доставая Б1, мы теряем возможность получить комбинацию Б2Б1, а доставая Б2 - теряем Б1Б2. Точно так же, как, если нам достался ящик с белым и черным шарами, мы автоматически потеряли возможность получить комбинацию ЧБ, достав белый шар. Вероятность ЧБ по условию вообще равна 0. Если мы изначально взяли контейнер с черным и белым шарами (вероятность 1/2), а затем согласно условию достали оттуда белый шар, то у нас остается только вариант с черным шаром.

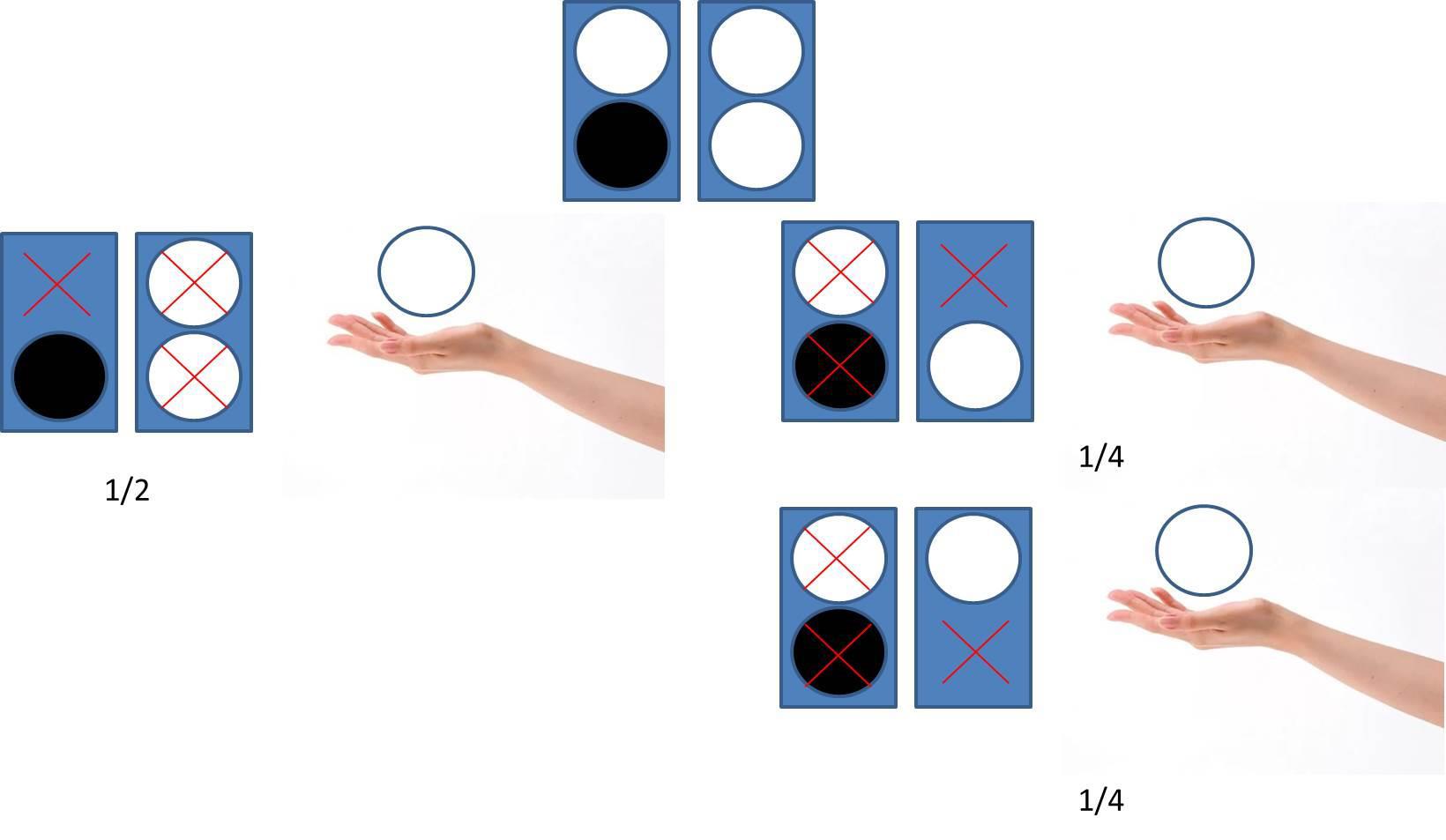
Вероятность достать вторым белый шар, таким образом, равна 1/4+1/4=1/2. Она была бы равна 2/3, только если бы нас не ограничивало условие "брать второй шар из того же ящика". Или если бы все шары лежали в общей куче. Тогда нам были бы доступны всего 3 шара, из которых 2 - белые. А не 2 шара, из которых 1 - черный. 

Еще вероятность 2/3 можно получить, исказив условие до "берем бесконечное число выборок по 2 ящика, в каждой открываем по ящику и достаем по 1 шарику, убираем все ящики, из которых извлекли черный шар". В этом случае отсеется 1/2 ящиков с черным и белым шарами. Соответственно, ящиков с белыми шарами будет не столько же, а в два раза больше, чем ящиков с черным и белым шарами. 

Так поступают решатели задачи с пирожками, которые получают 4/7. Если им предложить вариант той же задачи (7 яблочных пирожков, 5 малиновых, взяли наугад контейнер, в нем обнаружился яблочный пирожок, нужно найти вероятность, что второй тоже будет яблочный) с тремя и более пирожками в контейнере, они могут и вероятность выше 100% получить, ничтоже сумняшеся. Ведь если с двумя пирожками и двумя контейнерами получается 4 комбинации, то с тремя пирожками и двумя контейнерами комбинаций может быть аж 12 (я1я2я3, я1я3я2, я2я1я3, я2я3я1, я3я1я2, я3я2я1, и то же самое во втором контейнере), хотя всего яблочных пирожков при этом остается семь. 

Здесь вероятность, что в контейнере с одним яблочным пирожком окажется 3 яблочных пирожка, - 2/3, а никак не 12/7!

Не искажая условие, т.е. вначале выбрав наугад контейнер, в котором есть определенные предметы, затем узнав, что в нем есть предмет с конкретными свойствами (а не выбрав контейнер по принципу "из него первым достали такой-то предмет"), мы далее имеем дело с контейнером и с возможными комбинациями в рамках одного контейнера. А не со всеми возможными комбинациями в рамках всех контейнеров изначальной выборки или, тем паче, всех возможных выборок из всех возможных контейнеров. 

Апд: для совсем не понимающих, наверное, можно попробовать изменить цвет шаров. Представим, что в 2 ящиках лежат 4 шара. 2 белых, 1 синий, 1 черный. Один белый лежит с синим, один с черным. Из наугад выбранного ящика достали белый шар. Какова вероятность, что второй шар - синий? Хотя, думаю, некоторые оригиналы и эту задачу бы исказили...

Апд2: еще один альтернативный вариант задачки, с дверями, доказывает, что у людей с придумыванием аналогов все-таки проблемы. Аналог, обыгрывающий условие с белым шаром, - это "в комнате 4 двери, две белых на левой стене ведут в комнату слева, белая и черная на правой ведут в комнату справа. В белую дверь можно войти, но она сразу закрывается, так что выходить надо из второй. Черная открывается только на выход. Броском монетки выбираешь левую или правую стену, в одну дверь заходишь, в другую выходишь. Какова вероятность, что выйдешь в центральную комнату из белой двери?".

P.S. А еще мне теперь понятно, откуда берутся люди, которые выстраивают план на куче мелких допущений и верят, что если уж половина допущений реализовалась, то и последние вопросы решатся в их пользу)