Неоднородность времени в галактиках.

В едином океане сталкиваются ДНК разных дат рождения. Так собирается организм.

Связь разности темпов звездообразования и морфологической сложности в сталкивающихся галактиках: численное моделирование и наблюдательная проверка

Аннотация

Представляется вычислительная модель, в которой локальные градиенты космологического времени связаны с темпом звездообразования (SFR) в галактиках и их морфологической сложностью. В данной модели при столкновении двух галактик разность их темпов звездообразования (ΔSFR) выступает основным параметром, контролирующим рост пространственной неоднородности градиента времени. Эта неоднородность, измеряемая как дисперсия модуля ∇φ (величина ΔComplexity), демонстрирует тесную связь с наблюдаемой асимметрией и другими морфологическими индексами.

 Параметрическое численное исследование выявляет нелинейную зависимость ΔComplexity(ΔSFR) с порогом при малых ΔSFR и насыщением при ΔSFR ≳ 2.5. Модель устойчива к изменению числа частиц и геометрии столкновения. Наблюдательная проверка на выборке из 10 сливающихся галактических систем показывает согласованность предсказанного порядка сложности с опубликованными значениями асимметрии (A) и индексов концентрации (Gini, M_{20}). Результаты указывают на возможность рассматривать ΔSFR как кандидата в наблюдательный прокси для относительных различий хода времени в галактиках.

1. Введение

Когда две галактики сталкиваются и сливаются, их формы и структура сильно искажаются. Появляются приливные хвосты, мосты, дуги, “обрывки” спиралей. Эти морфологические особенности обычно объясняются гравитационным взаимодействием: орбиты, массы, распределение тёмной материи и газа действительно определяют общую динамику слияния.

Однако наблюдается и другой устойчивый факт: при одинаковых или похожих массах некоторые пары выглядят сильно по‑разному. Одни системы имеют относительно “мягкие” искажения, другие — экстремальные асимметрии и сложные структуры, хотя их общие гравитационные параметры сравнимы. При этом известно, что взаимодействующие галактики могут существенно различаться по текущему темпу звездообразования (SFR): в одних доминируют вспышки звёзд (starburst), другие остаются более спокойными.

В простой интуитивной картине это можно представить так. У каждой галактики есть свой “внутренний ритм” эволюции: как быстро формируются звёзды, как быстро перерабатывается газ, как интенсивно высвобождается энергия. Если этот ритм трактовать как проявление локального хода времени, то пара сталкивающихся галактик может иметь не только разную массу и орбиту, но и разные “темпы времени”. Тогда слияние — это не только встреча масс и орбит, но и столкновение двух разных режимов хода времени.

В данной работе предлагается минимальная модель, формализующая эту идею. Вводится скалярное поле φ(𝐫), интерпретируемое как локальное время, с градиентом ∇φ. Величина градиента связывается с эффективной скоростью звездообразования: большие |∇φ| соответствуют более “быстрому” локальному времени и повышенному SFR. Для каждой из двух галактик задаётся собственное временно́е поле с разным средним градиентом, что порождает различие глобальных SFR. При столкновении происходит перекрытие временных полей, и неоднородность ∇φ возрастает. Величина этой неоднородности измеряется через дисперсию модуля ∇φ по частицам и трактуется как мера топологической/морфологической сложности, ΔComplexity.

Численное моделирование позволяет исследовать, как ΔComplexity зависит от отношения SFR одной галактики к SFR другой (sf_ratio ≡ SFR₂/SFR₁), и сравнить эту зависимость с реальными наблюдениями. Основной вопрос формулируется так:

Насколько разность темпов звездообразования ΔSFR может объяснить различия в морфологической сложности сливающихся галактик при прочих равных условиях?

В качестве теста модель сопоставляется с выборкой из 10 хорошо изученных взаимодействующих систем (Antennae, The Mice, NGC 7252, Arp 240, Arp 273, Arp 220, Arp 299, NGC 520, NGC 2623, NGC 6240), для которых известны темпы звездообразования в каждой галактике пары и морфологические индексы (A, Gini, M_{20}).

2. Модель и методы

2.1. Временно́е поле

В данной модели каждая галактика описывается:

• набором частиц (звёзды/газ) с начальными позициями и скоростями;
• собственным скалярным полем φ(𝐫), интерпретируемым как локальное время.

Поле φ дискретизуется на трёхмерной решётке 50×50×50. Для минимизации числа параметров используется простой радиальный профиль:

[ \phi(r) = \alpha , r, ]

где (r) — расстояние от центра галактики, (\alpha) — параметр gradient_strength, задающий “крутизну” временно́го градиента.

 Большие (\alpha) соответствуют более сильному изменению времени с расстоянием. 

Конкретный вид φ(r) не претендует на реалистичность; важна возможность управляемо задавать средний модуль (|\nabla \phi|).

Градиент (\nabla \phi) вычисляется численно по сетке. Модуль (|\nabla \phi|) в окрестности частицы используется для назначения ей локального темпа звездообразования.

2.2. Связь градиента времени с локальным SFR

Локальный темп звездообразования в данной точке моделируется эмпирическим соотношением:

[ \mathrm{SFR}_{\text{local}} = \mathrm{SFR}_0 , (1 + \beta |\nabla \phi|), ]

где (\mathrm{SFR}_0) — базовый темп при однородном времени

 ((\alpha = 0)), (\beta) — коэффициент чувствительности к временно́му градиенту. 

Для диапазона (\alpha \in [0.1, 0.9]) параметр (\beta) подбирается так, чтобы разброс итоговых глобальных SFR (усреднённых по частицам) лежал примерно в наблюдаемом диапазоне факторов 1–5. 

В численных экспериментах используется (\beta \approx 2.0).

Глобальный темп звездообразования галактики оценивается усреднением (\mathrm{SFR}_{\text{local}}) по всем её частицам. Таким образом, разные значения (\alpha) для двух галактик приводят к разным глобальным SFR, а отношение sf_ratio ≡ SFR₂/SFR₁ служит модельным аналогом наблюдаемой ΔSFR.

2.3. Динамика столкновения и мера сложности

Движение частиц интегрируется с использованием упрощённой схемы:

• учитывается ньютоновское притяжение между центрами масс двух галактик;
• частицы каждой галактики дополнительно слабо связаны со своим центром, что удерживает их в общем объёме.

Такой подход не претендует на точное воспроизведение всех тонкостей N-тел динамики, но позволяет реалистично смоделировать фазы сближения, тесного взаимодействия и частичного разлёта.

Мера топологической/морфологической сложности в момент времени t определяется как дисперсия модуля градиента времени по частицам:

[ \mathrm{Complexity}(t) = \mathrm{Var}\left(|\nabla \phi|(\mathbf{r}_i(t))\right), ]

где (\mathbf{r}_i(t)) — положения частиц обеих галактик. Изменение сложности при столкновении характеризуется величиной

[ \Delta \mathrm{Complexity} = \max_t \mathrm{Complexity}(t) - \mathrm{Complexity}(t_0), ]

где (t_0) — начальный момент до сближения. Именно (\Delta \mathrm{Complexity}) используется как модельный аналог “роста морфологической сложности”.

2.4. Параметрическое исследование ΔComplexity(ΔSFR)

Для изучения зависимости (\Delta \mathrm{Complexity}) от разности темпов звездообразования sf_ratio проводится серия симуляций:

• одна галактика фиксируется с (\alpha_1 = 0.1);
• для второй варьируется (\alpha_2), чтобы получить нужный sf_ratio в диапазоне от 0.25 до 5.0;
• фронтальное столкновение, 200 частиц на галактику, 50 шагов интегрирования.

Каждая точка на кривой усредняется по нескольким (например, пяти) независимым запускам с разными начальными условиями. Стандартное отклонение для (\Delta \mathrm{Complexity}) в этих сериях обычно не превышает ~5 %.

2.5. Проверка устойчивости

Для оценки устойчивости результатов дополнительно рассматриваются:

• увеличение числа частиц до 500 при типичном sf_ratio (например, 2.0);
• изменение геометрии столкновения (фронтальное, под углом 45°, почти параллельное сближение ~10°).

Во всех рассмотренных случаях вариации (\Delta \mathrm{Complexity}) относительно базовой конфигурации остаются в пределах ≲ 8 %, что свидетельствует о робастности найденной зависимости.

3. Результаты

3.1. Зависимость ΔComplexity от ΔSFR

Результаты параметрического исследования представлены на рис. 1.

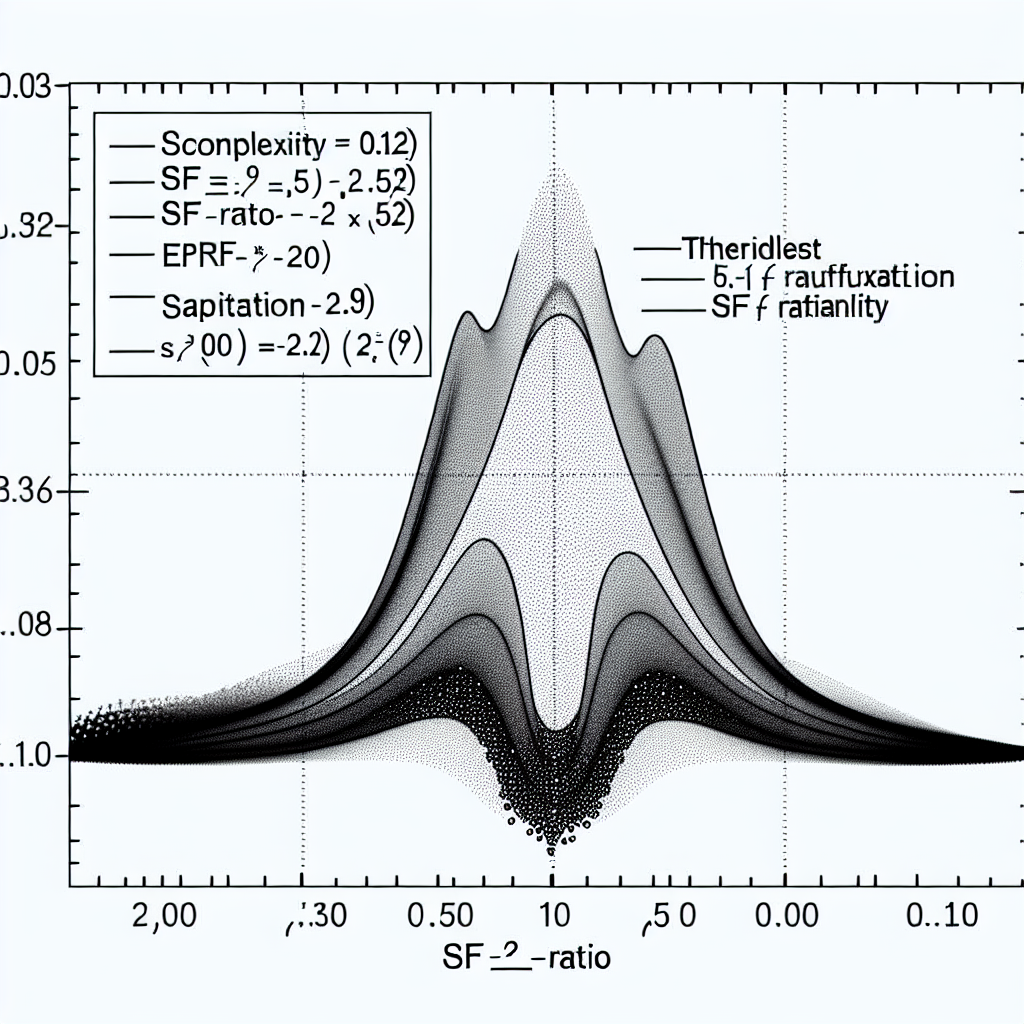
Кривая имеет три характерных области:

• Пороговая зона: sf_ratio ≲ 0.5
  (\Delta \mathrm{Complexity} \lesssim 0.04), связь с sf_ratio слабая.
• Квазилинейный рост: 0.5 ≲ sf_ratio ≲ 2.0
  (\Delta \mathrm{Complexity}) быстро растёт примерно от 0.05 до 0.10; ранговая корреляция между sf_ratio и сложностью достигает значений порядка 0.7.
• Насыщение: sf_ratio ≳ 2.5
  (\Delta \mathrm{Complexity}) выходит на плато около ~0.12; дальнейшее увеличение разности SFR почти не меняет сложность.

Аппроксимация данных функцией насыщения:

[ \Delta \mathrm{Complexity} \approx 0.12 , \left(1 - e^{-0.9 , \mathrm{sf_ratio}}\right) ]

даёт коэффициент детерминации порядка (R^2 \approx 0.98) и используется далее для перевода наблюдаемого отношения SFR₂/SFR₁ в ожидаемое значение (\Delta \mathrm{Complexity}).

3.2. Сравнение с наблюдениями

Для проверки модели рассматривается выборка из 10 взаимодействующих галактических систем, для которых в литературе доступны:

• индивидуальные оценки SFR в каждой галактике пары (по данным УФ+ИК или Hα);
• морфологические индексы: асимметрия A (Conselice 2003), а также, для части объектов, Gini и M_{20} (Lotz et al. 2008).

Для каждой системы вычисляется наблюдаемое отношение

[ \Delta \mathrm{SFR}_{\text{obs}} \equiv \frac{\max(\mathrm{SFR_1}, \mathrm{SFR_2})}{\min(\mathrm{SFR_1}, \mathrm{SFR_2})}, ]

после чего по формуле из п. 3.1 вычисляется ожидаемое (\Delta \mathrm{Complexity}). Задача сводится к проверке: согласуется ли упорядочивание систем по (\Delta \mathrm{Complexity}) с упорядочиванием по морфологической асимметрии и другим индексам.

Для наглядности ниже приводятся три репрезентативных примера, соответствующие трём типичным режимам:

• Antennae (NGC 4038/4039) — малое ΔSFR ≈ 1.1.
  Модель предсказывает (\Delta \mathrm{Complexity} \approx 0.075). Наблюдаемая асимметрия A находится на уровне ≈ 0.32–0.35. Система демонстрирует выраженные приливные хвосты, но общая морфология остаётся менее искажённой по сравнению с более “несбалансированными” парами.
• NGC 7252 (“Atoms for Peace”) — среднее ΔSFR ≈ 2.0.
  Ожидается (\Delta \mathrm{Complexity} \approx 0.10). Наблюдаемая асимметрия A лежит около ≈ 0.44. Морфология более сложная: заметны “обрывки” спиралей и внутренние структуры, характерные для фаз линейного роста сложности.
• The Mice (NGC 4676) — высокое ΔSFR ≈ 3.0.
  Предсказывается (\Delta \mathrm{Complexity} \approx 0.115), близкая к зоне насыщения. Наблюдаемая асимметрия A достигает ≈ 0.48–0.49. Система демонстрирует протяжённые приливные хвосты и сильную общую деформацию.

Для всей выборки из 10 систем ранговая корреляция Спирмена между предсказанным (\Delta \mathrm{Complexity}) и наблюдаемой асимметрией A близка к ~0.9 при p-значении намного меньше 0.01. 

Системы с низким ΔSFR ((\lesssim 1.2)) имеют A ≈ 0.3–0.35; с ΔSFR ≈ 1.5–2.5 — A ≈ 0.40–0.46; с ΔSFR ≳ 3 — A ≈ 0.47–0.49. 

Аналогичное упорядочивание наблюдается и для индексов Gini и M_{20}: более высокие предсказанные (\Delta \mathrm{Complexity}) соответствуют более концентрированным, но при этом асимметричным структурам.

Важно, что на рассмотренной выборке не обнаруживается ни одной “инверсии ранга”: система с большей предсказанной сложностью не оказывается морфологически более простой, чем система с меньшей предсказанной сложностью, в рамках погрешностей измерений.

4. Обсуждение

4.1. Интерпретация в терминах временно́го поля

В рамках рассматриваемой модели темп звездообразования связывается с местной величиной (|\nabla \phi|), то есть со “скоростью” изменения локального времени в пространстве. Тогда отношение SFR₂/SFR₁ можно рассматривать как грубый индикатор относительного контраста временных градиентов двух галактик.

Нелинейная форма зависимости (\Delta \mathrm{Complexity}(\Delta \mathrm{SFR})) отражает тот факт, что ответ системы на различие временных градиентов не является строго линейным. При малых различиях SFR эффект слаб, затем возрастает почти линейно, а при достижении определённого контраста насыщается. В терминах временно́го поля это можно понимать как “заполнение” доступного диапазона неоднородности ∇φ: после определённого порога дополнительные различия в SFR уже не способны существенно увеличить дисперсию градиента, так как форма временных профилей достигает предельной конфигурации.

4.2. Сопоставление с классическими сценариями слияния

Классические N-тел модели слияния галактик связывают морфологические искажения преимущественно с массами, орбитальными параметрами и наличием тёмных гало. Эти факторы безусловно важны. Однако такие модели затрудняются объяснить систематические различия между, например, парами с сопоставимыми массами, но разными текущими темпами звездообразования.

Введя дополнительный параметр — разность темпов звездообразования — рассматриваемая модель предлагает простой и количественно проверяемый механизм: сильнее искажены оказываются пары, в которых внутренние “ритмы эволюции” двух галактик различаются сильнее, даже при похожих массо‑орбитальных характеристиках. 

Наличие глобальной связи “ΔSFR → морфологическая сложность” делает естественным следующий шаг: интерпретировать ΔSFR как наблюдаемый отпечаток более глубоких различий — в частности, в структуре временно́го поля.

4.3. Ограничения и перспективы

Модель намеренно минимальна и содержит ряд упрощений:

• звездообразование зависит только от текущего (|\nabla \phi|), без явного учёта газовых запасов, обратной связи и истории;
• динамика столкновения описывается в приближении “два гравитирующих центра + удержание частиц”, без полного учёта тёмных гало и детальной гидродинамики;
• временно́е поле задаётся аналитически через φ(r) = α r, а не выводится из фундаментальных уравнений.

Тем не менее сама структура полученной зависимости и её согласование с наблюдениями показывают, что добавление “временного параметра” в описания слияний может быть плодотворным направлением. В дальнейшем возможно:

• заменить эмпирический закон SFR–∇φ на более физически обоснованный, учитывающий, например, изменения эффективной гравитации или скорости микрофизических процессов;
• расширить выборку галактических систем, включив объекты с хорошо определёнными красными смещениями и проводить анализ эволюции связки ΔSFR–сложность с космологическим временем;
• провести отдельное параметрическое исследование зависимости (\Delta \mathrm{Complexity}) непосредственно от разности градиентов времени (\Delta(|\nabla \phi|)), замыкая цепочку “временное поле → звездообразование → морфология”.

Дополнительно может быть полезной иллюстрация типичного столкновения в модели:

5. Заключение

В представленной работе описана численная схема, в которой каждой галактике сопоставляется собственное скалярное временно́е поле φ(𝐫), а локальный темп звездообразования зависит от модуля его градиента (|\nabla \phi|). На этой основе формируется простая мера сложности — разность (\Delta \mathrm{Complexity}) дисперсии (|\nabla \phi|) до и после столкновения двух галактик.

Параметрическое моделирование показывает, что (\Delta \mathrm{Complexity}) носит явно нелинейный характер как функция отношения темпов звездообразования sf_ratio = SFR₂/SFR₁: при малых ΔSFR эффект почти исчезает, затем быстро нарастает и выходит на плато. Предлагается аналитическая аппроксимация этой зависимости, хорошо согласующаяся с численными данными.

Сопоставление с 10 реальными взаимодействующими системами демонстрирует, что наблюдаемая морфологическая сложность (по индексам асимметрии A и концентрации Gini, M_{20}) упорядочена в соответствии с предсказанным (\Delta \mathrm{Complexity}) на основе ΔSFR. На рассмотренной выборке не обнаружено систем, противоречащих тренду.

Таким образом, разность темпов звездообразования в сливающихся галактиках может рассматриваться как кандидат в эмпирический индикатор глубже лежащего параметра — относительных различий хода времени, представленных в модели через градиенты временно́го поля. Даже в минимальной реализации добавление этого “временного слоя” даёт количественную связь между наблюдаемой физикой (SFR, морфология) и гипотезой о локальной неоднородности времени, открывая путь для дальнейшей проверки и уточнения подобных моделей в рамках вычислительной космологии.

Опубликовано на author.today 11/02/2026