Шо, опять про баллистику?

Я свою ошибку признал. А он устраивает развесёлое глумление в своём блоге, хотя ещё полгода назад писал мне, как хороши мои программы. И никакой ошибки с влиянием ветра он тогда в них не находил. Жил в плену тех же самых заблуждений, которые нынче высмеивает громче всех.
Цветной текст изменен и добавлен в день публикации блога, собственно в нём всё и пояснено

— - - далее текст того дня без изменений - - -

Как назвать, когда человек знает правду, но намеренно вводит другого в заблуждение? На днях одного хорошего человека намеренно ввели в заблуждение по части баллистики:

Но ведь Morceleb прекрасно знает, что именно так оно и есть. И считает он по той же формуле, об этом сам же писал в своих статьях. А тут вдруг - да может забыл внезапно?

Он был одним из первых, с кем я тут на этом сайте начал общаться. И поначалу общение шло нормально. Особенно же мы казалось бы сдружились по части этой самой баллистики. И формулы у нас были естественно одни и те же. В частности вот моя простая в использовании и очень наглядная программка, ну прям как игра, где можно провести осаду любого замка, какой Вам в своей книге захочется обстрелять из любого старинного орудия, начиная от примитивного рычажного камнемёта и заканчивая той самой мортирой6

наглядная баллистика
Осада замка 
http://steamage.ru/prog/bombarda/

Ветер влияет на снаряды - на любые, любой формы и веса. И влияет ровно настолько, какова скорость ветра. Не верите - любой учебник баллистики Вам об этом поведает. А теперь вот простая задачка: мортира выстреливает ядро со скоростью 100 м/с под углом 75° к горизонту, время в полёте округлим до 20 секунд. В безветрие упадёт через 510 м. Но дует встречный лёгкий ветерок, скорость 5 м/с. На сколько сместится ядро под влиянием ветра?

Ответ: 5 м/с * 20 с = 100 м. На целых сто метров (или на 20% дистанции выстрела) ветер успеет сдуть ядро мортиры, за то время, что ядро летит по воздуху к цели. Причём ветерок-то мы взяли слабенький, такой каждый день бывает, а Вы гуляете и даже его не замечаете.

Утверждение выше считать неверным! Спасибо Олегу Казакову, он там ниже в комментариях подсказал интересную мысль насчёт учёта разности плотностей. У кого есть ещё соображения = пишите в комментарии. У кого есть готовая формула - вообще было бы замечательно

Очень рекомендую не верить мне на слово, а воспользоваться программой
Осада замка 
http://steamage.ru/prog/bombarda/ 
и пострелять там самому.
Ибо наука это эксперимент!

А теперь пусть подует не ветерок, но ветер. Типичный для морского побережья или американских равнин ветер от 10 до 15 м/с. Нетрудно подсчитать, что за время полёта ядро сдует на дистанцию от 200 до 300 м. И это просто, как говорят моряки, свежий ветер, совсем не ураган, ураган начинается с 35 м/с. Но теперь читатель уже понимает, для артиллеристов и морской свежий ветер очень даже сильный.

То есть ветер легко может сдуть ядро мортиры на расстояние равное половине типичной дистанции стрельбы. 
Ещё у кого-то остались вопросы, нужно ли учитывать влияние ветра?

Сопротивления воздуха - в учебнике баллистики сказано: для скоростей снаряда до 200 м/с допускается при расчётах пренебрегать сопротивлением воздуха, поскольку погрешность составит считанные проценты и заведомо меньше радиуса компрессионного действия фугасного снаряда. Пусть даже мы стреляем не бомбой, а ядром. Но цель-то для мортиры не точка, а целый бастион! Размеры типичной цели принимали как квадрат 32 на 32 метра.

Средневековая мортира бьёт примерно на полкилометра, мортира первой половины XIX века до полутора километров. Да только на такую дальность разброс попаданий просто ужасный. Ствол-то был короткий, обтюрация между ядром и стенками ствола скверная, шанс попасть из мортиры на предельной дальности 5% - то есть лишь 1 выстрел из 20 попадёт в цель, при том что, напомню, цель здесь бастион.

Ясное дело никто в здравом уме на такие предельные дальности из мортир огонь не вёл, без крайней на то надобности. Стреляли так, чтобы попадал хотя бы каждый второй выстрел. А значит не далее вполне разумных 700 шагов - то есть по-нашему примерно полкилометра. На такой типичной дальности стрельбы погрешность от пренебрежения сопротивлением воздуха выйдет около 15 метров, что лишь половина от размера характерной цели для мортиры. А цель, напомню в третий раз - бастион. И если из расчётных 15 бомб в него попадёт лишь 10, то на общей картине боя это скажется незначительно, ведь главное мы уже определили - цель будет уверенно подавлена огнём.

А можно ли считать попроще? 
Когда ещё мы общались с Morceleb'ом, я пожаловался на свою неудачу с расчётом полёта снаряда с учётом сопротивления воздуха. Формула для этого есть в учебнике баллистики, она относится к концу XIX века и работам Маиевского, но даже столь великий баллистик прошлого не смог оставить потомкам математический инструмент, способный указать положение снаряда для попадания в точку. Собственно вот та формула:

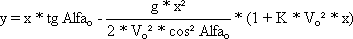
Я так же рассказал, что для подбора коэффициента использовал таблицу стрельбы 82-мм батальонного миномёта. Эта таблица составлена не по вычислениям, а по реальным отстрелам. Увы, подобрать коэффициент для точного расчёта не удаётся. Если сходится при стрельбе на максимальную дальность, то будет расхождение при стрельбе на половинную дистанцию. Подбираем, чтобы сошлось на середине, убегает крайняя точка. Формула несовершенна. И самое неприятное для историка - чтобы по ней считать, нужно прежде откуда-то раздобыть таблицы реального отстрела интересующей пушки. А кто даст пострелять скажем из Царь-пушки? Вот такая у нас, историков, беда.

На это Morceleb заявил, что он давно эту задачу решил, да и вообще чего там решать-то? Учесть сопротивление воздуха? Ха! Школьник справится. Какой на фиг генерал-инженер Маиевский? Учитесь, как надо.

На поверку же выяснилось, что Morceleb подошёл к задачке действительно как школьник - через вектора. Возможно это звучит очень круто, да только отчего-то учебник баллистики подобную методику расчётов не рекомендует. Может баллистики не дураки? Может есть причина, почему вектора тут не годятся?

Есть. Я сам писал расчёт и через вектора - например, на моём сайте SteamAge.ru есть

забавная игра
Krieg der Kokos 
http://steamage.ru/game/rodesia/

Но то игра, там точность не нужна. Главное веселуха, а через вектора считается очень просто, в самом деле и школьник справится. Но если сравнить точный расчёт по векторам или, как полагается по учебнику баллистики, по формуле описывающей функцию траектории полёта снаряда, то увидим различия:

• точность вычисления через вектора сильно зависит от заданной частоты дискретизации - чем она ниже, тем более ужасающая погрешность (поставьте дискретизацию в 1 секунду и сами увидите, как пуля трёхлинейки "пролетит" лишних полтора километра, вот такая ничего-себе-ошибочка)
• как следствие, при векторном вычислении максимальная дальность стрельбы выйдет при угле возвышения несколько менее 45° - тогда как в реальности несколько больше 45°

Именно так и вышло в вычислениях Morceleb'а - но странный результат не насторожил его. Напротив, он принял его как истинный.

Это пока мы считали без сопротивления воздуха. Morceleb смело это сопротивление добавил. Но откуда он взял его величину?

На это есть ответ в его статьях (ссылки не даю, статьи можно найти в его профиле и, если желаете разобраться, то нужно прочесть все, тщательно сверяя где и что именно написано), где он пространно рассуждает о характере трения воздуха на разные части снаряда в полёте - но не даёт ни одной цифры! Зато между делом оговаривается, что коэффициент-то взят некий общий для всего снаряда и усреднённый (к чему тогда были предшествующие рассуждения о сложном характере обтекания? видимо для солидности - ну что ж, к солидности претензий нет). И, решая задачу в лоб, предлагает по-школьному просто отнять/прибавить.

А вот каковы сугубо приблизительные ориентировочные коэффициенты для формулы Маиевского из учебника баллистики:

• K = 0.00000001 - для чугунного ядра
• K = 0.0000001 - для мушкетной пули
• K = 0.000001 - для стрелы лука
• K = 0.00001 - для пластикового шарика калибра 6-мм для игрушечного пневматического пистолета

Да это же такой мизер, что и прибавлять/отнимать нечего. А он и не прибавляется - ещё раз напомню формулу:

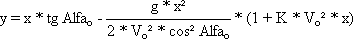
Коэффициент перемножается на квадрат скорости, да ещё и на дальность, прибавляется к единице - и лишь затем на него умножается результат вычислений. Но зачем так сложно-то?

А затем, что с дальностью падает и скорость - а чем ниже скорость, тем менее влияние сопротивления!

Простая формула с векторами этого никак не учитывает. Решение в лоб порочно само по себе, а с примесью неведомо как полученных коэффициентов... Впрочем, почему неведомо как? Очень даже ведомо. Ведь сам Morceleb и рассказывает об этом в своих статьях. Прикинул на глазок, вроде похоже получилось. На том и успокоился, сверять по таблицам стрельбы не стал.

Пока мы общались, я пытался донести до Morceleb'а, что его расчёт не даёт требуемой точности - и лучше уж тогда считать по классической формуле без учёта сопротивления воздуха, как и считали вполне успешно почти до конца XIX века. И позже пытался донести. Но, как обычно, он знает истину лучше всяких дурацких учебников (а теперь жутко обижается, когда оказывается что кто-то эти учебники хотя бы читал).

А если серьёзно это не столько про баллистику, сколько про реальную трагедию, которая развернулась вот тут, на этом сайте, прямо на наших глазах.

Был человек, ещё полгода назад с ним общаться можно было. Но что же потом с ним произошло?

Началось с малого. Он упрекал, что не знаю я про меткую стрельбу из древнего штуцера на 600 м - а потом оказалось, что он глянул в русско-язычный перевод и успокоился на этом, а в английском оригинале речь о 600, да только не метрах, а всего лишь футах. И когда это выяснилось, что же он сделал? Можно было извиниться, сказать ну погорячился, бывает. Он даже не признал своей ошибки. Или когда он яростно доказывал, что турки даже из рекордного лука не могли стрелять на 450 м, что стрела летит от силы лишь на 200 м - а оказалось сам в своих статьях писал, что турки даже из довольно рядовых луков стреляли более чем на 400 м, ну а его расчёт потенциала современных рекордных луков даёт цифру аж в 2 км (без учёта сопротивления воздуха, разумеется). И опять же вот это вскрылось, а он - в молчанку. А как он смеялся "Не бывает КПД более 100%, и тепловые насосы не могут иметь КПД 300%" - а с месяц назад глядь, уже пишет сам про тепловые насосы с эффективностью в 4 единицы (то есть 400% - ну хоть что-то полезное из общения со мной вынес, мне не жалко).

Я долго пытался выстроить заново нормальное общение. Да, тогда я был сильно добрее, отправить человека в игнор для меня было личной катастрофой. Но хамство с матюками мне совсем не по душе. Всё, баста! Разошлись как в море корабли. Но он не успокоился. Даже наоборот, дело всё более выглядит так как будто отринутый поклонник внимательно следит за мной. И любой ценой жаждет привлечь моё внимание к себе. Типа: эй, ты про меня совсем забыл? а я тут чахну и скучаю

Однажды мне добрые люди написали - смотри, вот тут https://author.today/post/120477 раскритиковали твой подводный город. Собственно единственная претензия по делу, что надо бы предусмотреть подпорные колонны. Ну казалось бы так и напиши. Но нет, первая часть его блога высмеивает им же придуманный идиотский сюжет будущего произведения, который он приписал мне. Очень смешно придумать глупость, приписать её другому, а потом смеяться - да смеёшься над СВОЕЙ глупостью!

Кстати, кому интересно, его возражения я развеял полностью в Виды подводных городов

А дальше ещё хуже, заметил он что Анастасия Семенюта помогает мне с поиском интересных фактов про Эпоху Пара - и тут же написал ей в личку, а что писал можете прочесть вот здесь https://author.today/post/120441 (там в самом начале).

Ну и вот теперь ещё этот последний случай, когда прекрасно зная, что сопротивление воздуха для ядра мортиры несущественно в отличие от ветра - он сознательно решил выставить это как нечто смешное, лишь бы... Лишь бы что?