Хотите теории вероятностей?
Автор: Василий ЧобитокТут понаписал в одном месте, оставлю на память
Простейшая задачка, но, как оказалось, толпы вот таких: "Ладно я со своим МПГУ (и пофиг что ведущий педвуз страны), но человеку не смог доказать что он ошибается даже Физмат МГУ!" -- неспособны к решению подобных задач.
Воспользуемся классическим представлением с урнами и шарами.
Условие задачи
Дано: в одной урне два белых шара, в другой урне -- белый и черный.
Из наугад выбранной урны наугад достали один шар, он оказался белым.
Вопрос: какова вероятность того, что следующий шар из той же урны будет белым?
Предварительные пояснения и анализ задачи
Представим урны и шары графически.
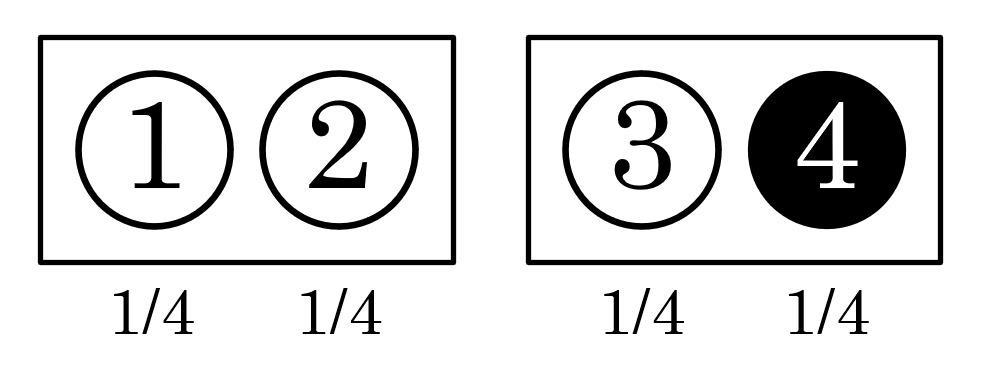
Нередко люди не понимают разницу между абстракцией "белый шар", обозначающей любой белый шар, и конкретным белым шаром (кто знаком с программированием: это как не понимать различие между классами и экземплярами классов). Чтобы избежать такого недопонимания, шары на схеме пронумерованы и здесь "белый шар" это любой из шаров №№ 1, 2 или 3.
Если произошло событие Ш "достали шар" (без уточнения цвета), то это может быть любой из 4-х, эти события равновозможны и вероятность для каждого из них Р(Ш) = 1/4.
Через полную группу событий. Четыре шара составляют полную группу событий, сумма их вероятностей 1, для равновозможных событий: Р(Ш) = 1/4.
Для тех, кто посчитал, что проигнорированы урны: вероятность выбрать урну Р(У) = 1/2, вероятность выбрать один из двух шаров в урне Р(Ш|У) = 1/2, соответственно: Р(Ш) = Р(У) × Р(Ш|У) = 1/2 × 1/2 = 1/4.
Рассмотрим событие Б "достали первым белый шар".
Введем обозначения:
1, 2, 3 -- события "достали шар" для шаров № 1, 2, 3
Б -- событие "достали белый шар"
У1, У2 -- события выбора урны 1 (левой) или 2 (правой)
Б1, Б2 -- события "достали белый шар" из урны 1 и 2
Пояснения:
1) всего шаров 4, из них белых 3, вероятность Р(Б) = 3/4;
2) белые шары входят в полную группу независимых событий,
поэтому Р(Б) = Р(1) + Р(2) + Р(3) = 1/4 + 1/4 + 1/4 = 3/4;
3) кто снова потерял урны, с урнами то же самое: Р(Б) = Р(У1)×Р(Б1) + Р(У2)×Р(Б2) = 1/2×1 + 1/2×1/2 = 3/4.
1-е решение задачи
Достали белый шар, но какой именно -- неизвестно, значит это может быть один из трёх шаров 1, 2 или 3.
Следующим можно извлечь шар только из той же урны, что и предыдущий, поэтому для трёх шаров получаем пары трех равновозможных (см. схему выше -- Р(Ш) для каждого из шаров равны) исходов:
1 -- 2 (второй белый)
2 -- 1 (второй белый)
3 -- 4 (второй черный)
Эти три пары составляют полную группу возможных исходов.
4-й шар черный, его случай не удовлетворяет условию задачи, поэтому из трех возможных исходов, благоприятствующих два.
Ответ: 2/3
2-е решение задачи
Воспользуемся решением через условную вероятность (желающие могу почитать учебники по теме).
Р(У1) = 1/2 -- вероятность выбрать левую урну с двумя белыми шарами (для данной задачи равнозначно двум белым шарам подряд)
Р(Б) = 3/4 -- вероятность выбора белого шара при первой попытке (см. выше)
Р(У1 | Б) -- условная вероятность "вероятность выбора левой урны при условии, что первый шар белый" (то же самое, что "второй шар белый")
Р(У1 | Б) = Р(У1) / Р(Б) = 1/2 : 3/4 = 2/3
Ответ: 2/3
3-е решение задачи (добавлено)
Для тех, кто думает, что первоначальные вероятности в решении неприменимы.
Поскольку полную группу первого исхода "достали белый шар" составляют шары 1, 2, 3, первоначальные вероятности достать которые были равны, то теперь вероятность того, что достали именно этот шар также равны и составляют по 1/3.
Остались возможными исходы:
1 -- 2 -- Р(1 и 2) = 1/3
2 -- 1 -- Р(2 и 1) = 1/3
3 -- 4 -- Р(3 и 4) = 1/3
Р(У1 | Б) = Р(1 и 2) + Р(2 и 1) = 1/3 + 1/3 = 2/3
Ответ: 2/3
Иллюстрация к решению 3
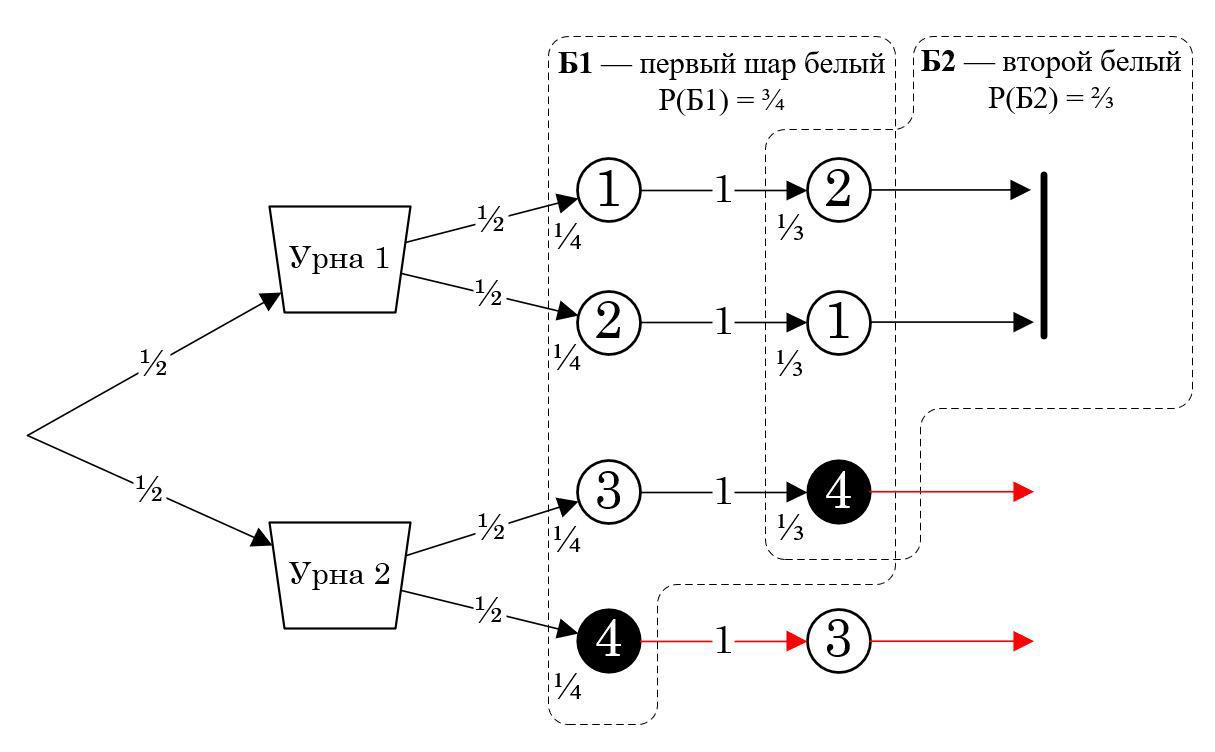
Есть и другие варианты решения задачи, но остановимся пока на 3-х
См. также иллюстрацию, которая предельно наглядно демонстрирует правильный ход решения.
Как решать эту задачу НЕправильно
Уверен, что среди присутствующих таких нет, но есть такие индивидумы, назовём их "тупыми курицами", которые подобные задачи решают следующим образом.
Тупая курица не понимает разницу между понятием "белый шар" в принципе и конкретным объектом "белый шар" (№№ 1, 2, 3), поэтому для нее "достали белый шар" в случае первой урны, это всегда шар № 1. Впрочем, тупая курица даже по рисунку не понимает, что левый и правый белые шары разные, поэтому не догадается пронумеровать их для упрощения и получит следующее:
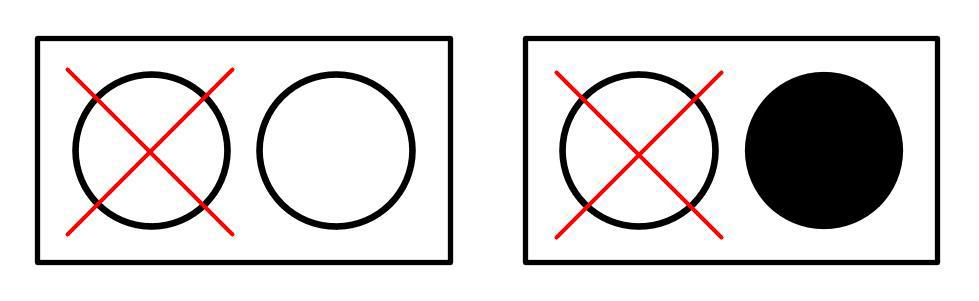
Первыми у тупой курицы могут быть извлечены только шары № 1 в левой урне или № 3 в правой. Шар № 2, невзирая на случайный порядок выбора шаров, у нее извлекается исключительно вторым.
Именно поэтому число возможных исходов она ассоциирует с числом урн -- у нее "осталось по одному шару в каждой урне", а значит ответ 1/2, потому что белый шар один из 2-х.
Тупая курица не решает задачу "достали белый шар", она решает задачу "достали шар № 1 или № 3".
Если число шаров в левой урне увеличить на 98 белых, а в правой на 98 черных, то у тупой курицы ответ так и останется 1/2.
Поэтому, дорогой товарищ, не надо быть ни такой же тупой курицей, ни волосатым пухляшом (что бы это ни значило).
UPD от 5.09.2024
Получающие в результате 1/2 решают задачу в таком условии:
В желобах белые шары всегда укладываются первыми. В один желоб уложили два белых шара, в другой -- белый и черный. Из случайного желоба достали первый шар. Какова вероятность того, что следующий шар тоже белый?
И для этого условия в самом деле ответ 1/2.
UPD.
Варианты решения более сложной задачи про пирожки из учебника.
