Хотите еще теории вероятностей?

Как оказалось, даже для такой элементарной задачи, как в предыдущей записи, из-за проблем с абстрактным мышлением очень многие не могут возможные исходы абстрагировать от урн и отождествляют их.

Предыдущая заметка

В качестве дополнения я придумал иллюстрацию, которая поможет хоть кому-то (сначала написал "многим", нет, волосатым пухляшам, мокрым курицам и пр. чудам природы не поможет) разобраться в правильном решении.

Исходная задача

Дано: в одной урне два белых шара, в другой урне -- белый и черный.
Из наугад выбранной урны наугад достали один шар, он оказался белым.
Вопрос: какова вероятность, что следующий шар из той же урны будет белым?

Задача имеет такую иллюстрацию:

Решения здесь приводить не буду, они есть в предыдущей заметке. Просто констатирую, что верный ответ 2/3.

Но есть большое число сторонников версии ответа 1/2, они считают, что если достать один белый шар, то для каждой урны будет по одному возможному исходу (один шар достали -- второй остался).

Аргумент, что в левой урне два белых шара и первым достать можно любой из них, а это два исхода, -- не принимается, потому что: "белый достали и белый остался -- вариант один, откуда два?!"

Попробую на примере модифицированной задачи показать как это работает.

Модифицированная задача

Дано: в одной урне стене две белых шара двери*, в другой урне стене -- белая и красная.
На наугад выбранной урны стене наугад достали один шар выбрали дверь**, она оказалась белой.
Вопрос: какова вероятность, что шар из той же урны будет белымследующая за выбранной дверь будет белой?

* двери одной стены соединены коридором: войдя в одну дверь, выйдешь через вторую на той же стене.

** для особо одаренных, которые посчитают, что видимая дверь в стене никак не может быть аналогом шара в урне. Шар достается вслепую, т.е. случайно, дверь тоже можно выбрать случайно, например броском монеты. Это в равной мере случайный выбор из двух вариантов.

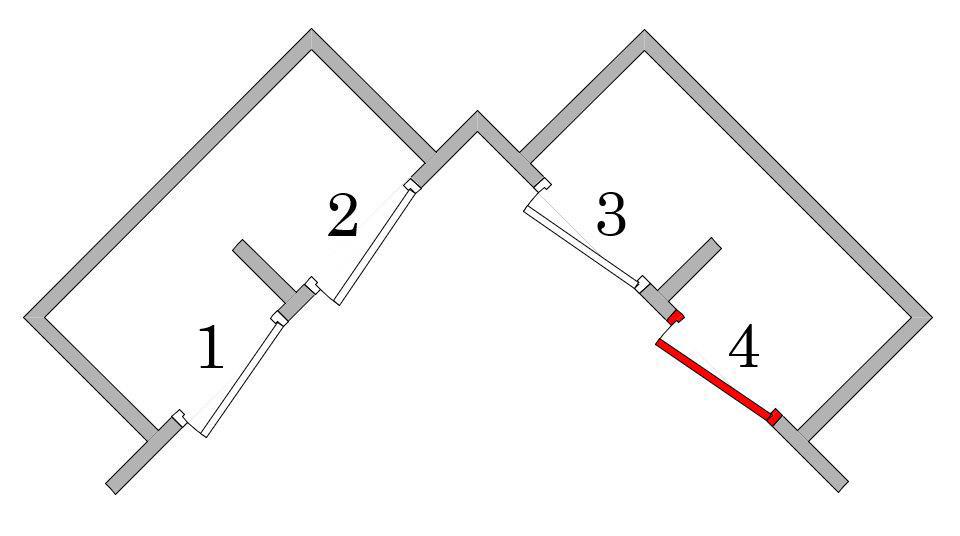
Если дверь выбирается случайно без ограничений по цвету, то у нас 4 маршрута:

1--2
2--1
3--4
4--3

Правда, с дверьми намного понятнее? Да, в обоих вариантах маршрута с дверьми 1 и 2 мы проходим "две белые двери", но утверждать, что пройти эти двери можно только одним способом (маршрутом) возьмется только особо альтернативно одаренный.

Когда же стало известно, что выбранная дверь белая, то остаются маршруты:

1--2
2--1
3--4

Их три! И только два из них благоприятствующие. Ответ на задачу: 2/3.

P.S. Предвижу возражения, что это другая задача, другие условия... Только для умственно отсталых! С точки зрения теории вероятности это совершенно, абсолютно та же сама задача, которую, как завещал профессор Пискунов (кстати, тоже танкист), можно свести к "схеме урн", т.е. задаче из предыдущего сообщения.