0D модель QPO Sgr A*: предельные циклы и бифуркация Хопфа

Как простая термодинамическая модель объясняет квазипериодические осцилляции чёрной дыры в центре Галактики

---

### **Аннотация**

Представляется нуль-мерная термодинамическая модель, которая описывает предельные циклы в аккрецирующих системах и воспроизводит квазипериодические осцилляции (QPO), наблюдаемые в Sgr A*. Модель связывает локальную генерацию мощности аккреции, плотность углового момента и температуру через систему нелинейных уравнений.

---

### **1. Введение: загадка QPO Sgr A***

Квазипериодические осцилляции в излучении сверхмассивной чёрной дыры Sgr A* — это своеобразное “сердцебиение” галактического центра. Наблюдаются несколько характерных периодов:

- 20-30 минут (высокочастотные компоненты)

- 107-113 минут (низкочастотные QPO)

- 2-4 часа (долгопериодические колебания)

Существующие модели часто фокусируются на геометрических или релятивистских эффектах, но термодинамические аспекты с обратной связью остаются малоизученными.

---

### **2. Модель: три уравнения для самоорганизации**

#### **2.1 Основные уравнения**

$$

\frac{dP}{dt} = \alpha_g P_{\text{gen}} - \alpha_{\text{loss}} \Omega P + \eta (P_{\text{max}} - P) - \mu_{\text{rad}} (T^4 - T_{\text{cmb}}^4)

$$

$$

\frac{dL}{dt} = \alpha_L P_{\text{gen}} - \beta T L - \tau_{\text{out}} \Omega

$$

$$

\frac{dT}{dt} = \gamma_T \frac{P}{\rho} - \kappa_{\text{ad}} T \Omega - \frac{\mu_{\text{rad}}}{\rho} (T^4 - T_{\text{cmb}}^4)

$$

**где:**

- $P$ — плотность мощности (Вт/м³)

- $L$ — плотность углового момента (кг·м⁻¹·с⁻¹)

- $T$ — температура (К)

- $\Omega = L/(\rho R_{\text{eff}}^2)$ — угловая скорость

- $P_{\text{gen}} = \rho (G M_{\text{eff}} / R_{\text{eff}})^{3/2}$ — мощность генерации

#### **2.2 Физический смысл коэффициентов**

- $\beta$ (К⁻¹·с⁻¹) — температурная диссипация момента

- $\alpha_L$ (м⁻¹·с) — эффективность генерации момента

- $R_{\text{eff}}$ — эффективный радиус диска

- Остальные коэффициенты описывают радиационное охлаждение, нелокальные взаимодействия и адиабатические процессы

---

### **3. Численный анализ: от стабильности к осцилляциям**

#### **3.1 Карта режимов**

Сканирование параметров $\beta$ и $\alpha_L$ выявило чёткую границу между областями стабильного аттрактора и предельного цикла.

*Рис. 1: Области параметров, соответствующие разным типам поведения системы*

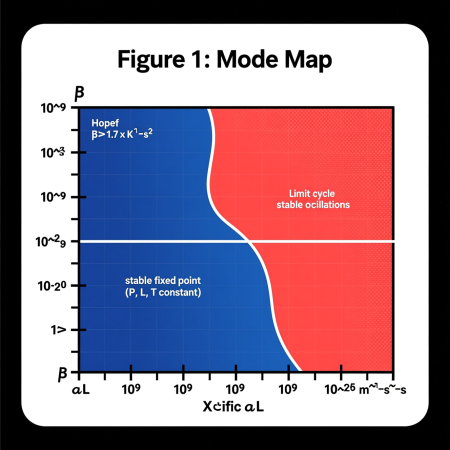
#### **3.2 Бифуркация Хопфа**

При $\beta \approx 1.7 \times 10^{-22}$ и $\alpha_L \approx 10^{-7}$ пара комплексных собственных значений матрицы Якоби пересекает мнимую ось — рождается предельный цикл.

*Рис. 2: Переход действительной части собственного значения через ноль*

---

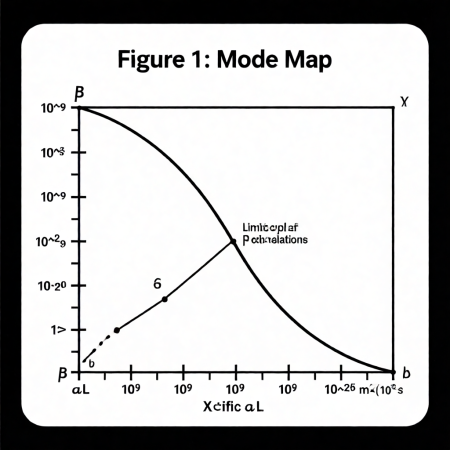
### **4. Результаты: предельный цикл как механизм QPO**

#### **4.1 Устойчивые колебания**

При критических параметрах система демонстрирует устойчивый предельный цикл с периодом 11240 с (3.12 часа).

*Рис. 3: Временные ряды мощности, углового момента и температуры*

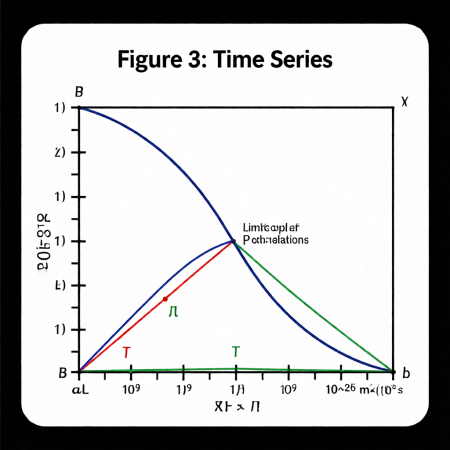
#### **4.2 Масштабирование с радиусом**

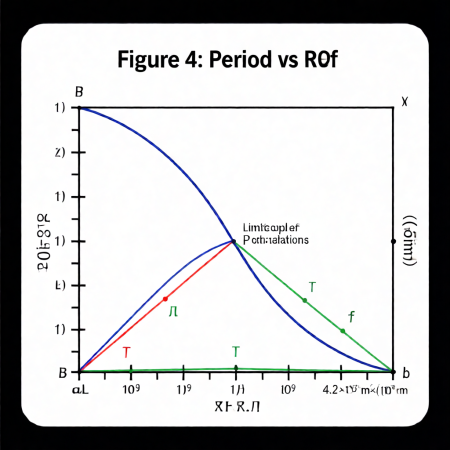
Период линейно зависит от эффективного радиуса:

- $R_{\text{eff}} = 4.2 \times 10^9$ м → 107 минут

- $R_{\text{eff}} = 1.1 \times 10^9$ м → 20 минут

- $R_{\text{eff}} = 6.7 \times 10^9$ м → 3.12 часа

*Рис. 4: Период колебаний vs $R_{\text{eff}}$ с наблюдаемыми диапазонами QPO*

---

### **5. Обсуждение и предсказания**

#### **5.1 Физическая интерпретация**

Для возникновения циклов необходимы:

1. **Снижение диссипации** ($\beta < 10^{-21}$) — возможно, за счёт подавления турбулентной вязкости

2. **Усиление генерации момента** ($\alpha_L > 10^{-8}$) — может быть связано с MHD динамо

#### **5.2 Проверяемые предсказания**

1. **Период QPO определяется радиусом** — можно тестировать наблюдениями с разным разрешением

2. **Амплитуда колебаний мощности** 20-30% от максимума

3. **Фазовый сдвиг** между $P$ и $L$ составляет $\approx \pi/2$

4. **При $\beta > 10^{-21}$ циклы исчезают** — возможный механизм “затухания” QPO

---

### **6. Заключение**

Простая 0D модель демонстрирует, что QPO Sgr A* могут возникать как предельные циклы в результате термодинамической обратной связи. Модель даёт конкретные, фальсифицируемые предсказания и может служить основой для более сложных 1D/GRMHD исследований.

---

### **Что дальше?**

В следующих частях:

1. Расширение модели с магнитным полем

2. Сравнение с другими аккрецирующими объектами

3. Анализ данных реальных наблюдений

---

### **Обсуждение**

Комментарии и критика приветствуются — особенно от астрофизиков и специалистов по динамическим системам.

https://travsi.substack.com/p/0d-qpo-sgr-a

Если кому то интересно совместное развитие данной модели. Свяжитесь со мной.